Ta có  − a x + y = 3 x + 1 + y = 2

⇔ y = a x + 3 | x + 1 | + a x + 3 = 2 ⇔ y = a x + 3 | x + 1 | + a x + 1 = 0

Nếu x ≥ − 1 ta có x + 1 + ax + 1 = 0 ⇒ x(a + 1) = −2   (1)

Phương trình (1) có nghiệm duy nhất ⇔ a ≠ −1 x = − 2 a + 1 ⇒ y = a + 3 a + 1

  x ≥ − 1 ⇔ − 2 a + 1 ≥ − 1 ⇔ − 2 a + 1 + 1 ≥ 0 ⇔ a − 1 a + 1 ≥ 0 ⇔ a − 1 a + 1 ≥ 0 a ≠ − 1 ⇔ a ≥ 1 a < − 1

Nếu a < −1 ta có –x – 1 + ax + 1 = 0 ⇒ (a – 1)x = 0    (2)

Nếu a = 1 thì (2) là 0x = 0 đúng với mọi x < −1 nên (2) có vô số nghiệm hay hệ đã cho có vô số nghiệm (loại)

Nếu a ≠ 1 thì (2) có nghiệm duy nhất x = 0 (loại so x < −1). Do đó (2) vô nghiệm khi a ≠ 1

Để hệ phương trình đã cho có nghiệm duy nhất thì có 2 trường hợp:

Trường hợp 1: Phương trình (1) vô nghiệm và phương trình (2) có nghiệm duy nhất

Trường hợp này không xảy ra vì (2) chỉ có thể vô nghiệm hoặc vô số nghiệm

Trường hợp 2: Phương trình (1) có nghiệm duy nhất và phương trình (2) vô nghiệm  ⇔ a ≥ 1 a < − 1 a ≠ 1 ⇔ a > 1 a < − 1

Đáp án:B

Từ hệ được x+y=1

a)Thay vào được x=1;y=0

b)Với mọi a

c)Thay vào x+y=1 tìm x;y

Thay ngược vào hệ tìm a

a) Khi a = 2 hệ phương trình đã cho tương đương với:

 \(\hept{\begin{cases}x+2x=3\left(1\right)\\2x-y=2\left(2\right)\end{cases}}\Leftrightarrow\hept{\begin{cases}3x=3\\2x-y=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\2x-2=y\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\2.1-2=0=y\end{cases}}\)

Do vậy \(\left(x;y\right)=\left(1;0\right)\)

b) Ta có:  \(x+y=\left(x+ax\right)-\left(ax-y\right)=3-2=1>0\forall a\)

c) Lấy (1) trừ (2),vế với vế,ta có: \(x+y=1\)

Thay vào,ta có: \(\sqrt{2}.y+y=1\Leftrightarrow y\left(\sqrt{2}+1\right)=1\)

\(\Rightarrow y=\frac{1}{\sqrt{2}+1}\Rightarrow x=1-\frac{1}{\sqrt{2}+1}=\frac{\sqrt{2}}{\sqrt{2}+1}\)

Thay vào hệ phương trình ban đầu,ta có: \(\hept{\begin{cases}\frac{\sqrt{2}}{\sqrt{2}+1}+\frac{\sqrt{2}}{\sqrt{2}+1}.a=3\left(3\right)\\\frac{\sqrt{2}}{\sqrt{2}+1}.a-\frac{\sqrt{1}}{\sqrt{2}+1}=2\left(4\right)\end{cases}}\)

Lấy (3) + (4),vế với vế,ta có: \(\frac{2\sqrt{2}}{\sqrt{2}+1}.a=5\Leftrightarrow a=\frac{10+5\sqrt{2}}{4}\)

Thay \(a=-\sqrt{2}\) vào pt :

\(\left\{{}\begin{matrix}\left(-\sqrt{2}+1\right)x-y=3\left(1\right)\\-\sqrt{2}x+y=-\sqrt{2}\left(2\right)\end{matrix}\right.\)

Lấy \(\left(1\right)+\left(2\right):\) 

\(\left(-\sqrt{2}+1-\sqrt{2}\right)x=3-\sqrt{2}\)

\(\Leftrightarrow x=\dfrac{3-\sqrt{2}}{1-2\sqrt{2}}\)

\(\Leftrightarrow x=\dfrac{1-5\sqrt{2}}{7}\)\(\left(3\right)\)

Thay \(\left(3\right)\) vào \(\left(2\right)\) : \(-\sqrt{2}.\dfrac{1-5\sqrt{2}}{7}+y=-\sqrt{2}\)

\(\Rightarrow y=\)\(-\sqrt{2}+\dfrac{6\sqrt{2}}{7}\)

\(\Rightarrow y=-\dfrac{\sqrt{2}}{7}\)

Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(\dfrac{1-5\sqrt{2}}{7};-\dfrac{\sqrt{2}}{7}\right)\)

- Để hệ phương trình có nghiệm duy nhất

\(\Leftrightarrow\dfrac{a}{1}\ne-\dfrac{1}{a}\)

\(\Leftrightarrow a^2\ne-1\) ( Luôn đúng )

Vậy mọi a thuộc R hệ phương trình luôn có 1 nghiệm duy nhất .

- Ta có : \(\left\{{}\begin{matrix}y=ax-2\\x+a\left(ax-2\right)=3\end{matrix}\right.\)

- Từ PT ( II ) => \(x+xa^2-2a=3\)

\(\Rightarrow x=\dfrac{2a+3}{a^2+1}\)

- Thay lại x vào PT ( I ) ta được : \(y=\dfrac{a\left(2a+3\right)}{a^2+1}-2\)

\(=\dfrac{2a^2+3a-2a^2-2}{a^2+1}=\dfrac{3a-2}{a^2+1}\)

Vậy ...

Ta có: D = 2 − 1 1 2 = 5 ≠ 0

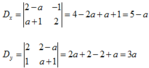
Vì D ≠ 0 nên hệ phương trình có nghiệm duy nhất

x = D x D = 5 − a 5 ;   y = D y D = 3 a 5

Khi đó:

x 2 + y 2 = 5 − a 5 2 + 3 a 5 2

= 25 − 10 a + 10 a 2 25 = 10 25 a 2 − a + 1 = 2 5 a − 1 2 2 + 9 10 ≥ 9 10

Dấu “=” xảy ra ⇔ a = 1 2

Đáp án cần chọn là: C