Cho đồ thị hàm số y = a x 2 + bx + c như hình vẽ.
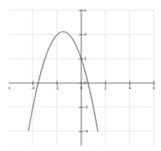
Khẳng định nào sau đây là đúng:
A. a > 0, b < 0, c > 0
B. a < 0, b > 0, c > 0
C. a < 0, b < 0, c < 0
D. a < 0, b < 0, c > 0
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
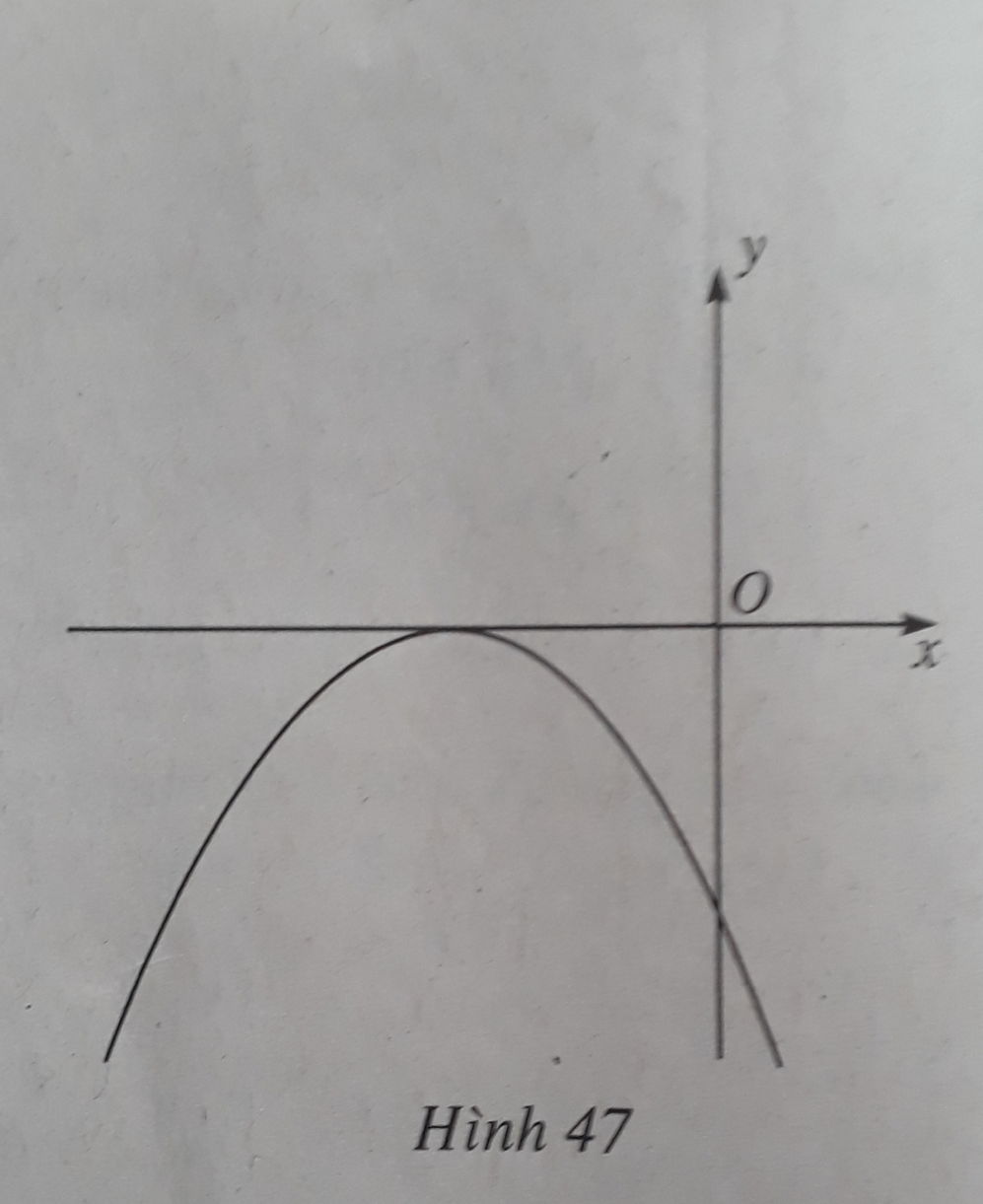
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
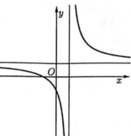
Hàm số y = b x - c x - a a ≠ 0 ; a , b , c ∈ ℝ có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
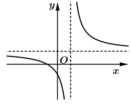
A. a > 0, b > 0, c - ab < 0
B. a > 0, b > 0, c - ab > 0
C. a > 0, b > 0, c - ab = 0
D. a > 0, b < 0, c - ab < 0
Đồ thị hàm số có tiệm cận đứng x = a > 0; tiệm cận ngang y = b > 0
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên
Cho hàm số y = b x - c x - a (a ≠ 0 và a,b,c ϵ ℝ) có đồ thị như hình bên dưới. Khẳng định nào dưới đây là đúng?
A. a > 0, c-ab < 0
B. a > 0,b > 0,c-ab > 0
C. a < 0,b> 0,c-ab < 0
D. a < 0,b < 0,c-ab > 0
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho biết hàm số y=ax^3 + bx^2 + cx + dy=ax3+bx2+cx+d có đồ thị như hình trên. Trong các khẳng định sau, khẳng định nào đúng?
\A.{a>0b2−3ac=0
B{a>0b2−3ac<0
C,,{a<0b2−3ac>0
D,,{a<0b2−3ac=0
Biểu thức tổng quát của hàm số có đồ thị như hình 1.6 là:
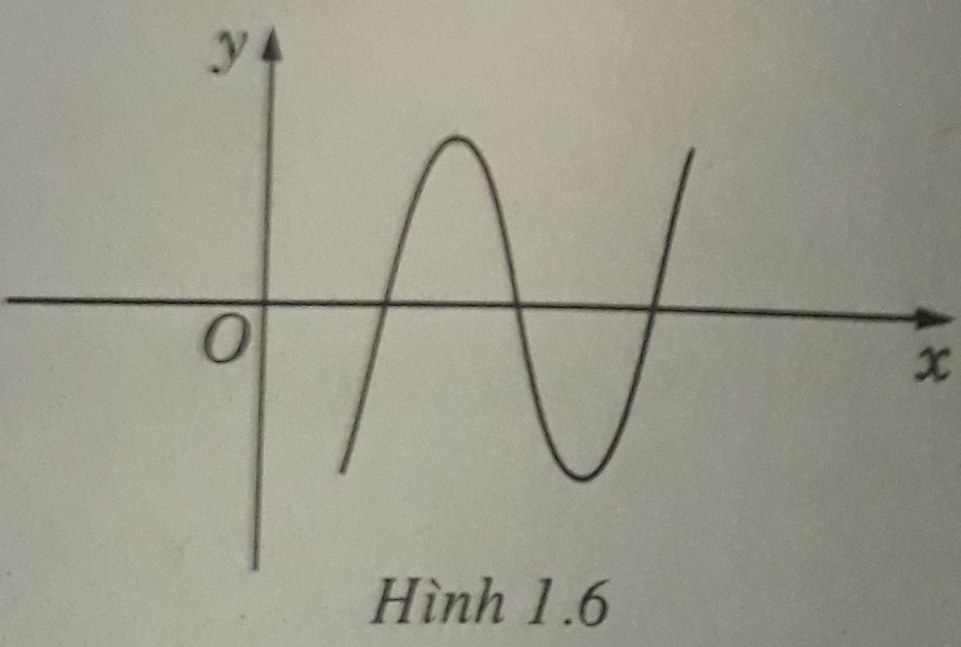
A. y = a x 2 + bx + c với a ≠ 0
B. y = a x 3 + cx + d với a < 0
C. y = a x 3 + b x 2 + cx + d với a > 0 và b 2 - 3ac > 0
D. y = x 3
Cho hàm số y = ax 3 + bx 2 + cx + d (a,b,c,d là các hằng số,a≠0) có đồ thị như sau:
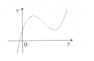
Khẳng định nào sau đây là khẳng định đúng?
A. abcd > 0.
B a–b+c+d < 0.
C. a–b+c+d > 0.
D. abcd = 0.
Cho hàm số y = a x 3 + b x 2 + c x + d (a,b,c,d là các hằng số,a ≠ 0) có đồ thị như sau:
Khẳng định nào sau đây là khẳng định đúng?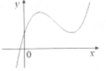
![]()
![]()
![]()
![]()
Nếu hàm số y = a x 2 + b x + x có a > 0 , b < 0 , c < 0 thì đồ thị của nó có dạng nào trong các hình sau?

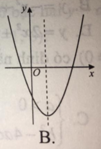
Ta có: x = − b 2 a > 0 nên trục đối xứng nằm bên phải trục Oy
Đồ thị cắt trục tung tại điểm (0; c) nằm dưới trục hoành ( vì c < 0).
Do đó, đồ thị B là đồ thị của hàm số đã cho.
Đáp án B
Cho 3 số a, b, c > 0, a ≠ 1 , b ≠ 1 , c ≠ 1 . Đồ thị các hàm số y = a x , y = b x , c = c x . được cho trong hình vẽ bên dưới. Mệnh đề nào sau đây đúng ?
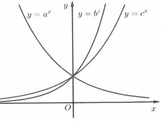
A. b < c < a
B. a < c < b
C. a < b < c
D. c < a < b
Ta vẽ đường thẳng x = 1 cắt các đồ thi hàm số đã cho tại tung độ lần lượt a; b; c
Vậy a < b < c. Chọn B