Các câu hỏi tương tự
Đồ thị hàm số
y
f
(
x
)
a
x
2
+
b
x
+
c
được cho trong hình 47. Kí hiệu
Δ
b
2
-
4
a
c
là biệt số của f(x). Trong các khẳng định sau, kh...
Đọc tiếp
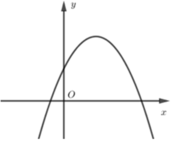
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
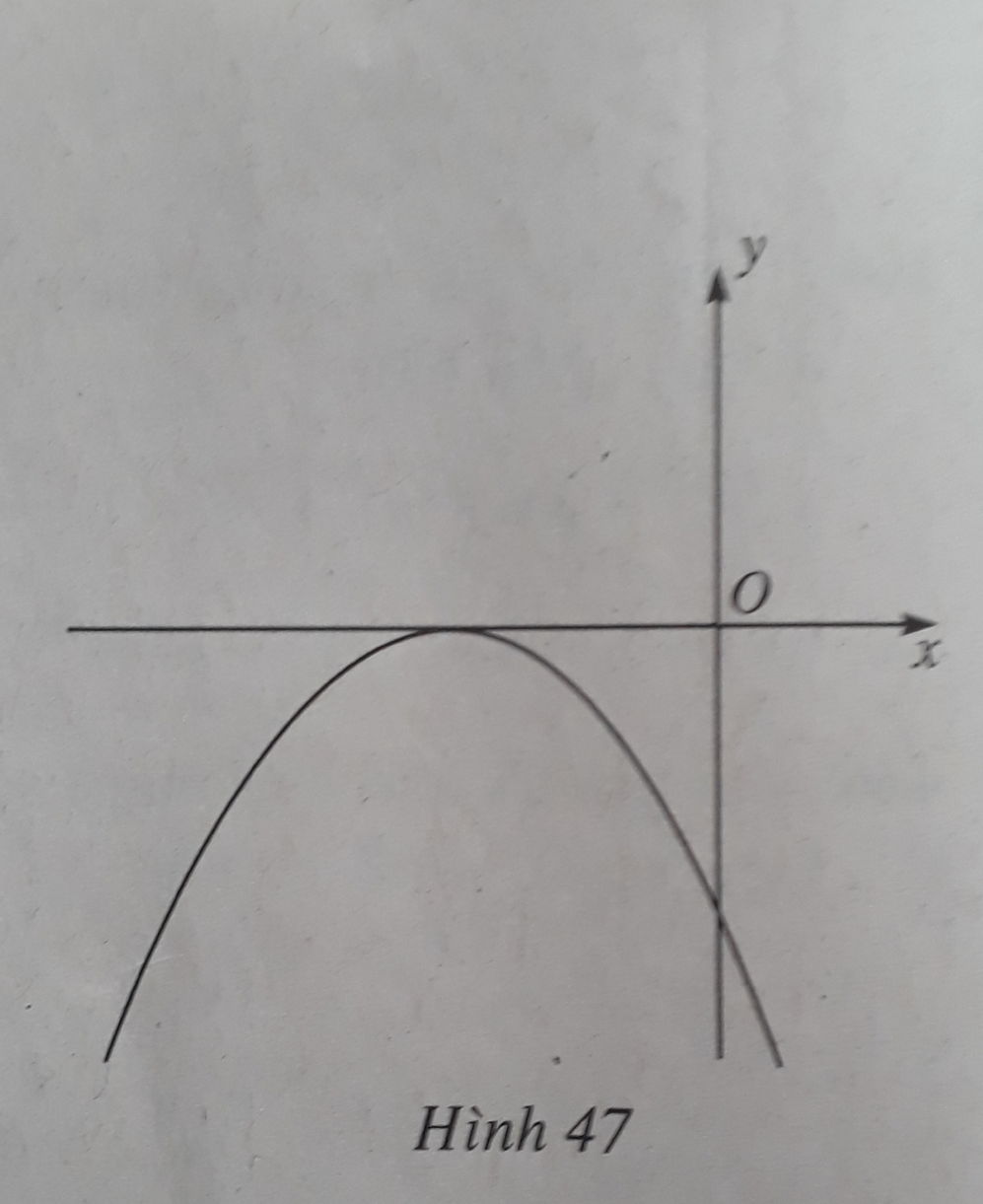
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
Nếu hàm số
y
a
x
2
+
b
x
+
x
có
a
0
,
b
0
,
c
0
thì đồ thị của nó có dạng nào trong các hình sau?
Đọc tiếp
Nếu hàm số y = a x 2 + b x + x có a > 0 , b < 0 , c < 0 thì đồ thị của nó có dạng nào trong các hình sau?

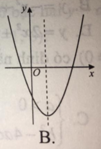
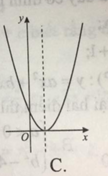
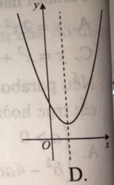
Nếu hàm số y a
x
2
+ bx + c có a 0,b 0 và c 0 thì đồ thị của nó có dạng A. B. C. D.
Đọc tiếp
Nếu hàm số y = a x 2 + bx + c có a < 0,b > 0 và c > 0 thì đồ thị của nó có dạng
A.
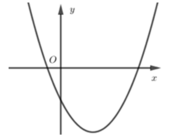
B.
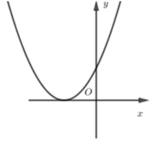
C.
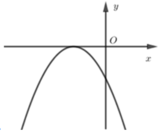
D.
Điểm nào sau đây thuộc đồ thị của hàm số
y
|
x
+
2
|
+
|
3
x
-
1
|
+
|
-
x
+
4
|
? A. M(0; 7) B. N(0; 5) C. P(-2; -1) D. Q(-2; 1)
Đọc tiếp
Điểm nào sau đây thuộc đồ thị của hàm số y = | x + 2 | + | 3 x - 1 | + | - x + 4 | ?
A. M(0; 7) B. N(0; 5)
C. P(-2; -1) D. Q(-2; 1)
Biết rằng hàm số y = a x 2 + bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; −1). Tính tổng S = a + b + c.
A. S = -1
B. S = 4
C. S = - 4
D. S = 2
Đồ thị hàm số y=3x-1 đi qua điểm có tọa độ nào sau đây?
A.
(0;−1)(0;−1)
B.
(2;−5)(2;−5)
C.
(0;3)(0;3)
D.
(−1;4)
Đồ thị (P) của hàm số y=x²+bx+c . Xác định b, c biết (P) đi qua A(-2 ;2) và B(0 ;5)
Cho góc b với 0 ◦ ≤ b ≤ 180◦ có điểm biểu diễn là B(0; 1). Khẳng định nào sau đây đúng? A. b = 10◦ . B. b = 90◦ . C. b = 0 ◦ . D. b = 180◦ .
[2] Cho hai tập hợp A = { x ∈ R | 3x -1 >= 2; 3-x > 1 }; B = [ 0; 3]. Khẳng định nào sau đay là đúng?
A. \(C_BA\) = { 0; 2; 3 } B. \(C_BA\) = [ 2; 3 ] C. \(C_BA\) = [ 0; 1 ) D. \(C_BA\) = [ 0; 1 ) ∪ [ 2; 3 ]
Cho phương trình của (P): y a
x
2
+ bx + c (a
≠
0) biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A (2; 0), B (−2; −8). Tình tổng
a
2
+
b
2
+
c
2
A.
a
2
+
b
2
+
c...
Đọc tiếp
Cho phương trình của (P): y = a x 2 + bx + c (a ≠ 0) biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A (2; 0), B (−2; −8). Tình tổng a 2 + b 2 + c 2
A. a 2 + b 2 + c 2 = 3
B. a 2 + b 2 + c 2 = 29 16
C. a 2 + b 2 + c 2 = 48 29
D. a 2 + b 2 + c 2 = 5 a 2 + b 2 + c 2 = 209 16