Cho hai đường tròn đồng tâm ( O;R) và (O; R’) với R ≠ R’,có bao nhiêu phép vị tự biến (O;R) thành (O; R’)
A. Vô số
B. 1
C.2
D. 3
Cho hai đường tròn (O) và (O') có cùng bán kính R cắt nhau tại hai điểm A, B sao cho tâm O nằm trên đường tròn (O') và tâm O' nằm trên đường tròn (O). Đường nối tâm OO' cắt AB tại H, cắt đường tròn (O') tại giao điểm thứ hai là C. Gọi F là điểm đối xứng của B qua O'.
a) Chứng minh rằng AC là tiếp tuyến của (O), và AC vuông góc BF.
b) Trên cạnh AC lấy điểm D sao cho AD = AF. Qua D kẽ đường thăng vuông góc với OC cắt OC tại K, Cắt AF tại G. Gọi E là giao điểm của AC và BF. Chứng minh các tứ giác AHO'E, ADKO là các tứ giác nội tiếp.
c) Tứ giác AHKG là hình gì? Vì sao.
d) Tính diện tích phần chung của hình (O) và hình tròn (O') theo bán kính R.
Cho đường tròn tâm O bán kính R và đường thẳng (d) cắt đường tròn tâm O tại hai điểm C và D (đường thẳng d không đi qua tâm O). Từ điểm S bất kì thuộc tia CD (S nằm ngoài đường tròn tâm O), kẻ hai tiếp tuyến SA và SB với đường tròn tâm O (với A và B là các tiếp điểm). Gọi H là trung điểm của đoạn CD và E là giao điểm của AB với SC. Chứng minh rằng: Khi S di chuyển trên tia CD (S nằm ngoài đường tròn tâm O) thì đường thẳng AB luôn đi qua 1 điểm cố định
cho hai đường tròn tâm O và O' tiếp xúc ngoài với nhau tại A, có đường kính AB của đường tròn tâm O, đường kính AC của đường tròn O', gọi MN là tiếp tuyến chung của hai đường tròn (M thuộc đường tròn O, N thuộc đường tròn O') hai tia BM và CN cắt nhau tại E. a) CM: tam giác EBC là tam giác vuông b) CM: EB.EM=EN.EC c) Tính MN biết bán kính của đường tròn (O) và (O') lần lượt là 9cm và 4cm
Cho hai đường tròn đồng tâm O. Một đường tròn (O’) cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D. Chứng minh rằng AB // CD.
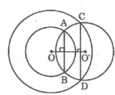
Vì đường tròn (O’) cắt đường tròn (O ; OA) tại A và B nên OO’ là trung trực của AB
Suy ra : OO’ ⊥ AB (1)
Vì đường tròn (O’) cắt đường tròn (O ; OC) tại C và D nên OO’ là trung trực của CD
Suy ra : OO’ ⊥ CD (2)
Từ (1) và (2) suy ra : AB // CD.
Cho hai đường tròn đồng tâm O. Một đường tròn (O') cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D.
Chứng minh rằng AB // CD ?
Cho 1 điểm M nằm bên ngoài đường tròn tâm (O) bán kính= 3 cm kẻ hai tiếp tuyến MN MB n p là hai tiếp điểm của đường tròn tâm (Ở) vẽ các tiếp tuyến của đường tròn tâm (O )sao cho đoạn AB = 3 cm với AB thuộc đường tròn tâm (O) A nằm giữa M và B. a,chứng minh tứ giác OPMN nội tiếp đường tròn b, gọi H là trung điểm của đường tròn OAB số sánh MON và MHN
Cho đường tròn tâm O bán kính 2cm trên đường tròn tâm O Lấy điểm O' vẽ đường tròn tâm O bán kính 2cm hai đường tròn này cắt nhau tại điểm A và B
đường thẳng OO'cắt đường tròn tâm O bán kính 2cm tại điểm thứ 2M và cắt đường tròn tâm O bán kính 2cm tại điểm thứ 2N.Tính MN
Cho hai đường tròn tâm O và tâm O' cắt nhau tại A và B cố định. Vẽ AC và AD là đường kính của đường tròn tâm O và O'. Một đường thẳng d thay đổi luôn đi qua A cắt đường tròn tâm O và đường tròn tâm O'lần lượt tại M và N. Xác định vị trí của d để CM + DN đạt giá trị lớn nhất.
Cho nửa đường tròn (O) đường kính AB . Lấy M là điểm tùy ý (H\(\varepsilon\)AB) . Trên cùng nửa mawtjj phẳng bờ AB chứa nửa đường tròn (O) vẽ hai đường tròn tâm O\(_1\), đường kính AH và tâm O\(_2\),đường kính BH , MA và MB cắt hai nửa đường tròn (O\(_1\))và (O\(_2\)) lần lượt tại P và Q. Chứng minh:
a) MH=PQ
b) Các tam giác MPQ và tam giác MBA đồng dạng;
c) PQ là tiếp tuyến chung của hai đường tròn (O\(_1\)) và (O\(_2\)).