Cho tứ diện ABCD. Gọi E; F; G là điểm lần lượt thuộc các cạnh AB; AC; BD sao cho EF cắt BC tại I; EG cắt AD tại H . Ba đường nào sau đây đồng quy?
A. CD; EF; EG
B. CD; IG; HF
C. AB; IG; HF
D. AC; IG; BD
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AB, AC; điểm E trên cạnh CD sao cho E D = 3 E C . Thiết diện tạo bởi mặt phẳng M N E và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEF với F là điểm bất kỳ trên cạnh BD
C. Hình bình hành MNEF với F là điểm trên cạnh BD với EF//BC
D. Hình thang MNEF với F là điểm trên cạnh BD sao cho EF//BC
Cho khối tứ diện ABCD. Gọi M, N, E lần lượt là trung điểm của AB, BD, DA. Tỉ số thể tích của khối tứ diện MNEC và ABCD bằng:
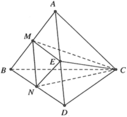
A. 1/4
B. 1/8
C. 1/2
D. 1/3
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD
C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC
D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Đáp án C
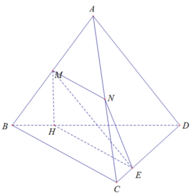
Xét (MNE) và (BCD) có:
E là điểm chung
BC // MN ⇒ BC // (MNE)
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua E và song song BC
d cắt BD tại H
⇒ MNEH là thiết diện cần tìm
Xét tứ giác MNEH có MN // EH ( // BC)
⇒ MNEH là hình thang
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C, D và M là trung điểm của đoạn thẳng AB. Gọi T là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T).
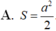
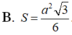
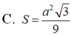
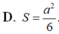
Đáp án D
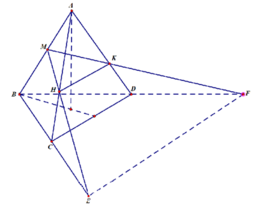
Thiết diện cần tìm là MHK
Ta có:
H là trọng tâm tam giác ABE
K là trọng tâm tam giác ABF
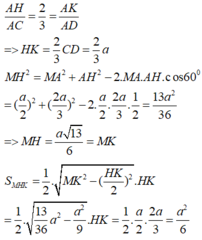
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
A. S = a 2 2
B. S = a 2 3 6
C. S = a 2 3 9
D. S = a 2 6
Đáp án D
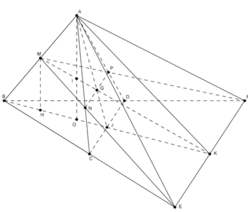

Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó
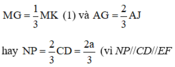
và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là


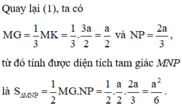
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C, D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T).
A. S = a 2 2 .
B. S = a 2 3 6 .
C. S = a 2 3 9 .
D. S = a 2 6 .
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
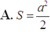


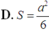
Đáp án D
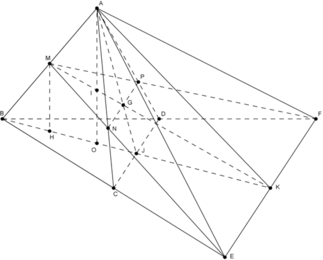
Vẽ AO ⊥ (BCD, MH ⊥ (BCD). Gọi K là trung điểm EF, ta có (ABK) ⊥ (BCD), mp (ABK) chứa AO, MH và là mặt phẳng trung trực của đoạn CD và EF.
Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó MG = 1 3 MK (1) và AG = 2 3 AJ hay NP = 2 3 CD = 2 a 3 (vì NP//CD//EF và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là 3 2 a (và diện tích là 3 4 a 2 ).
Tam giác đều BCD cạnh a có đường cao BJ = 3 2 a , trọng tâm O, suy ra BO = 2 3 BJ = a 3 . Lại vì MH là đường trung bình trong tam giác vuông ABO nên
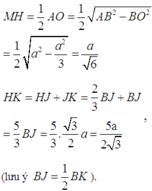
Vì tam giác MHK vuông tại H nên ta có
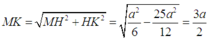
Quay lại (1), ta có
![]()
từ đó tính được diện tích tam giác MNP là
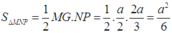
Cho tứ giác ABCD. E là giao điểm của AB và CD. Gọi F là trung điểm của AC, G là trung điểm của BD. Chứng minh diện tích tam giác EFG = 1/4 diện tích tứ giác ABCD.
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Biết diện tích của tứ giác ABCD là 18 m 2 thì diện tích của tứ giác EFGH là:
A. 9 m 2
B. 5 m 2
C. 6 m 2
D. 7 , 5 m 2
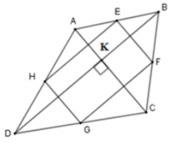
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)

Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Biết diện tích của tứ giác ABCD là 40 m 2 thì diện tích của tứ giác EFGH là:
A. 30 m 2
B. 25 m 2
C. 40 m 2
D. 20 m 2
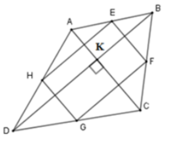
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)

Đáp án D