Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng có phương trình P : x − y + 4 z − 2 = 0 và Q : 2 x − 2 z + 7 = 0 . Góc giữa hai mặt phẳng (P) và (Q) là
A. 90 °
B. 45 °
C. 60 °
D. 30 °
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;0;1), B(1;2;3) và mặt phẳng (Q) có phương trình: x+y-z=0. Viết phương trình mặt phẳng (P).
A. − 4 x + 3 y − z + 1 = 0.
B. 4 x + 3 y + z - 1 = 0.
C. 3 y − z + 1 = 0.
D. 4 x + 3 y + 2 = 0.
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 3x+y+z-5=0 và (Q): x+y2+z-4=0. Khi đó, giao tuyến của (P) và (Q) có phương trình là
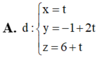
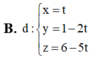
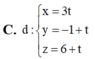
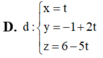
Đáp án D
Phương pháp giải:
Ứng dụng tích có hướng để tìm vectơ chỉ phương của đường thẳng giao tuyến và giải hệ phương trình để tìm tọa độ giao điểm của hai mặt phẳng
Lời giải: Ta có
![]()
Gọi d là giao tuyến của (P) và (Q).
Ta có
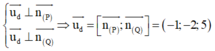
Xét hệ
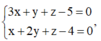
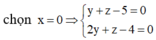
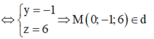
Vậy phương trình đường thẳng cần tìm là
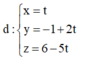
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 , d 2 lần lượt có phương trình d 1 : x - 2 2 = y - 2 1 = z - 3 3 ; d 2 : x - 1 2 = y - 2 - 1 = z - 1 4 . Mặt phẳng cách đều hai đường thẳng có phương trình là
A. 14 x - 4 y - 8 z + 1 = 0
B. 14 x - 4 y - 8 z + 3 = 0
C. 14 x - 4 y - 8 z - 3 = 0
D. 14 x - 4 y - 8 z - 1 = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x + y + z + 1 = 0 và hai điểm A 1 ; - 1 ; 2 , B 2 ; 1 ; 1 . Mặt phẳng Q chứa A, B và vuông góc với mặt phẳng P . Mặt phẳng Q có phương trình là:
A. - x + y = 0
B. 3 x - 2 y - z + 3 = 0
C. x + y + z - 2 = 0
D. 3 x - 2 y - z - 3 = 0
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng d : x 1 = y - 1 1 = z - 2 1 và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 = 0, (Q): x – 2y – 2 = 0
A . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
B . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
C . S : x + 1 2 + y + 2 2 + z + 3 2 = 5
D . S : x - 1 2 + y - 2 2 + z - 3 2 = 3
Chọn A
Gọi I là tâm mặt cầu (S). Khi đó I (t; 1+t; 2+t) và ta có:
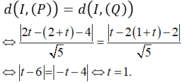
Vậy mặt cầu (S) có tâm I (1;2;3) và bán kính 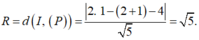
Do đó mặt cầu (S) có phương trình: ![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x-y+z-1=0 và (Q):2x+y+1=0. Viết phương trình mặt phẳng đi qua A(1;-1;-2) vuông góc với hai mặt phẳng (P) và (Q).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x–y+z -1= 0 và (Q):2x+y+1= 0. Viết phương trình mặt phẳng đi qua A(1;-1;-2) vuông góc với hai mặt phẳng (P) và (Q).
A. x+2y+3z+7=0.
B. x-2y+3z+3=0.
C. x+2y-3z–5=0.
D. x–2y–3z-9=0.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P = x + y + z − 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z − 2 − 1 . Đường thẳng d ' đối xứng với d qua mặt phẳng (P) có phương trình là
A. x + 1 1 = y + 1 2 = z + 1 7
B. x + 1 1 = y + 1 − 2 = z + 1 7
C. x − 1 1 = y − 1 2 = z − 1 7
D. x − 1 1 = y − 1 − 2 = z − 1 7
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y+z-4=0 và hai đường thẳng d 1 : x - 3 2 = y - 2 1 = z - 6 5 ; d 2 : x - 6 3 = y 2 = z - 1 1 . Phương trình đường thẳng d nằm trong mặt phẳng (P) và cắt hai đường thẳng d 1 , d 2 là:
A. x - 1 - 1 = y - 1 2 = z - 1 - 3
B. x - 1 2 = y - 1 - 3 = z - 1 - 1
C. x - 1 - 3 = y - 1 2 = z - 1 - 1
D. x - 1 2 = y - 1 - 1 = z - 1 - 3
Chọn B
Gọi A, B lần lượt là giao điểm của d1d2 với mặt phẳng (P). Đường thẳng d cần tìm đi qua A và B.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y+z-4=0 và hai đường thẳng d 1 : x - 3 2 = y - 2 1 = z - 6 5 , d 2 : x - 6 3 = y 2 = z - 1 1 . Phương trình đường thẳng d nằm trong mặt phẳng (P) và cắt hai đường thẳng d1, d2 là:
![]()
![]()
![]()
![]()