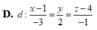Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x-y+z-10 và (Q):2x+y+10. Viết phương trình mặt phẳng đi qua A(1;-1;-2) vuông góc với hai mặt phẳng (P) và (Q).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x-y+z-1=0 và (Q):2x+y+1=0. Viết phương trình mặt phẳng đi qua A(1;-1;-2) vuông góc với hai mặt phẳng (P) và (Q).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+y+z-70 và đường thẳng
d
:
x
-
3
-
2
y
+
8
4
z
-
1
. Phương trình mặt phẳng (Q) chứa d đồng thời vuông góc với mặt phẳng (P) là...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+y+z-7=0 và đường thẳng d : x - 3 - 2 = y + 8 4 = z - 1 . Phương trình mặt phẳng (Q) chứa d đồng thời vuông góc với mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho
A
(
1
;
-
1
;
2
)
;
B
(
2
;
1
;
1
)
và mặt phẳng
(
P
)
:
x
+
y
+
z
+
1
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A ( 1 ; - 1 ; 2 ) ; B ( 2 ; 1 ; 1 ) và mặt phẳng ( P ) : x + y + z + 1 = 0 . Mặt phẳng ( Q ) chứa A , B và vuông góc với mặt phẳng ( P ) . Mặt phẳng ( Q ) có phương trình là:
A. 3 x - 2 y - z - 3 = 0
B. x + y + z - 2 = 0
C. - x + y = 0
D. 3 x - 2 y - z + 3 = 0
Trong không gian với hệ tọa độ Oxyz cho A(1;-1;2), B(2;1;1) và mặt phẳng (P): x+y+z+10. Mặt phẳng (Q) chứa A, B và vuông góc với mặt phẳng . Mặt phẳng (Q) có phương trình là: A. -x+y0 B. 3x-2y-z+30 C. x+y+z-20 D. 3x-2y-z-30
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho A(1;-1;2), B(2;1;1) và mặt phẳng (P): x+y+z+1=0. Mặt phẳng (Q) chứa A, B và vuông góc với mặt phẳng . Mặt phẳng (Q) có phương trình là:
A. -x+y=0
B. 3x-2y-z+3=0
C. x+y+z-2=0
D. 3x-2y-z-3=0
Trong không gian với hệ tọa độ Oxyz, cho điểm H(2; –1;2) là hình chiếu vuông góc của gốc tọa độ O xuống mặt phẳng (P). Số đo góc giữa mặt phẳng (P) và mặt phẳng (Q) có phương trình – y + z 0 là: A.
90
0
. B.
60
0
. C.
45
0
. D.
30
0
.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm H(2; –1;2) là hình chiếu vuông góc của gốc tọa độ O xuống mặt phẳng (P). Số đo góc giữa mặt phẳng (P) và mặt phẳng (Q) có phương trình – y + z = 0 là:
A. 90 0 .
B. 60 0 .
C. 45 0 .
D. 30 0 .
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) đi qua hai điểm A(0;1;0), B(2;3;1) và vuông góc với mặt phẳng (Q):x+2y-z0 có phương trình là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) đi qua hai điểm A(0;1;0), B(2;3;1) và vuông góc với mặt phẳng (Q):x+2y-z=0 có phương trình là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng
d
:
x
1
y
-
1
1
z
-
2
1
và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 0, (Q): x – 2y – 2 0
A
.
S...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng d : x 1 = y - 1 1 = z - 2 1 và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 = 0, (Q): x – 2y – 2 = 0
A . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
B . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
C . S : x + 1 2 + y + 2 2 + z + 3 2 = 5
D . S : x - 1 2 + y - 2 2 + z - 3 2 = 3
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 3x+y+z-50 và (Q): x+y2+z-40. Khi đó, giao tuyến của (P) và (Q) có phương trình là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 3x+y+z-5=0 và (Q): x+y2+z-4=0. Khi đó, giao tuyến của (P) và (Q) có phương trình là
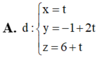
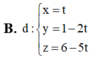
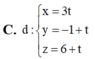
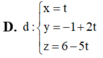
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng: (P): x + y + z - 2 0 (Q): x + 2y - z +3 0 và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P) và (Q).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz,
cho hai mặt phẳng:
(P): x + y + z - 2 = 0
(Q): x + 2y - z +3 = 0
và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P)
và (Q).
![]()
![]()
![]()