GIẢI HỘ MK VỚI Ạ / CẲM ƠN MỌI NGƯỜI RẤT NHIỀU

x2 + 4x + 3
mọi người tính hộ mk với ạ mai mk thi rồi ạ !
cảm ơn m.n nhiều !
\(x^2+4x+3=x^2+3x+x+3=\left(x^2+3x\right)+\left(x+3\right)=x\left(x+3\right)+\left(x+3\right)=\left(x+3\right)\left(x+1\right)\)
m.n giúp mk câu này vs ạ
(\(\dfrac{x+2}{x-2}-\dfrac{x-2}{x+2}+\dfrac{16}{4-x^2}\)) : (\(\dfrac{4}{2-x}-\dfrac{8}{2x-x^2}\))
Mọi người ơi, giải giúp em bài này với ạ. Em cảm ơn rất nhiều ạ!
Mọi người ơi, giải gấp các bài này giúp mình trong ngày hôm nay với ạ, mình cảm ơn mọi người rất nhiều ạ!!!
\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...
\(3,ĐK:x\ge-1\\ PT\Leftrightarrow3\left(x^2-x+1\right)-2\left(x+1\right)=5\sqrt{x^3+1}\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\)
\(PT\Leftrightarrow3b^2-2a^2=5ab\\ \Leftrightarrow2a^2+5ab-3b^2=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\a=-3b\left(vn\right)\end{matrix}\right.\Leftrightarrow a=2b\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\\x=\dfrac{5-\sqrt{37}}{2}\end{matrix}\right.\left(\text{giống bài 2}\right)\)
mọi người giải hộ e bài 1 với ạ e cảm ơn nhiều 
Mọi người ơi, mình chưa biết giải bài này:(( Mọi người giúp mình với, mình cảm ơn rất nhiều ạ😭 
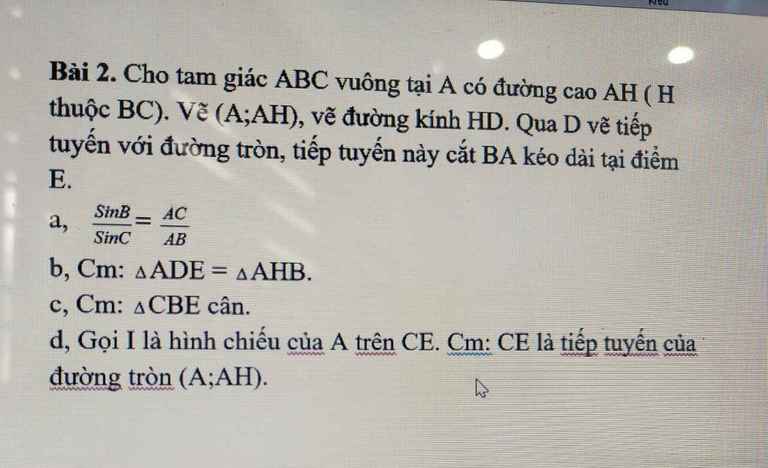
mọi người giúp mình caau d với ạ giải chi tiết nhé
mình cám ơn rất nhiều ạ
 Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều![]()
Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$
Bài 5:a)
Xét tam giác vuông $AHB$ và $AHC$ có:
$AB=AC$ (do $ABC$ là tam giác cân ở A)
$\widehat{ABH}=\widehat{ACH}$ (do tam giác $ABC$ cân ở A)
$\Rightarrow \triangle AHB=\triangle AHC$ (cạnh huyền- góc nhọn)
$\Rightarrow HB=HC$ và $\widehat{BAH}=\widehat{CAH}$ (đpcm)
b)
$HB=HC$ nên $H$ là trung điểm $BC$. Do đó $HB=BC:2=4$ (cm)
Áp dụng định lý Pitago:
$AH=\sqrt{AB^2-AH^2}=\sqrt{5^2-4^2}=3$ (cm)
c)
Xét tam giác vuông $ADH$ và $AEH$ có:
$AH$ chung
$\widehat{DAH}=\widehat{EAH}$ (do $\widehat{BAH}=\widehat{CAH}$)
$\Rightarrow \triangle ADH=\triangle AEH$ (cạnh huyền- góc nhọn)
$\Rightarrow DH=EH$ nên tam giác $HDE$ cân tại $H$.
Giải giúp mình câu 6vaf câu 7 với ạ. Cảm ơn mọi người rất nhiều
Mọi người ơi giải giúp mình 3 câu này với ạ, mình cảm ơn rất nhiều