thực hiện phép tính
(3xy-x-y2)2x
giúp với mọi người
Những câu hỏi liên quan
8 tháng 9 2021 lúc 17:58
Bài 2: Thực hiện các phép tính sau:
a)(x3+5x2-2x+1)(x-7)
b)(2x2-3xy+y2)(x+y)
c)(x-2)(x2-5x+1)-x(x2+11)
d)x(1-3x)(4-3x)-(x-4)(3x+5)
\(a,\left(x^3+5x^2-2x+1\right)\left(x-7\right)\\ =x^4-7x^3+5x^3-35x^2-2x^2+14x+x-7\\ =x^4-2x^3-37x^2+15x-7\\ b,\left(2x^2-3xy+y^2\right)\left(x+y\right)\\ =2x^3+2x^2y-3x^2y-3xy^2+xy^2+y^3\\ =2x^3-x^2y-2xy^2+y^3\\ c,\left(x-2\right)\left(x^2-5x+1\right)-x\left(x^2+11\right)\\ =x^3-5x^2+x-2x^2+10x--x^3-11x\\ =x^3-7x^2\\ d,x\left(1-3x\right)\left(4-3x\right)-\left(x-4\right)\left(3x+5\right)\\ =x\left(4-15x+9x^2\right)-\left(3x^2-7x-20\right)\\ =4x-15x^2+9x^3-3x^2+7x+20\\ =9x^3-18x^2+11x+20\)
Đúng 2
Bình luận (0)
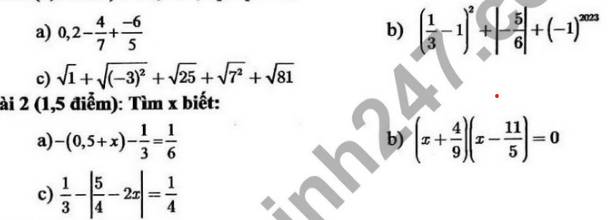bài 1: thực hiện phép tính
bài 2: tìm x
mọi người giúp mik với
Bài 1:
$0,2-\frac{4}{7}+\frac{-6}{5}=\frac{1}{5}+\frac{-6}{5}-\frac{4}{7}$
$=\frac{-5}{5}-\frac{4}{7}=-1-\frac{4}{7}=\frac{-11}{7}$
b.
$=(\frac{-2}{3})^2+\frac{5}{6}+(-1)=\frac{4}{9}+\frac{5}{6}-1$
$=\frac{8}{18}+\frac{15}{18}-1=\frac{23}{18}-1=\frac{5}{18}$
c.
$=1+3+5+7+9=25$
Đúng 0
Bình luận (0)
Bài 2:
a. $-(0,5+x)-\frac{1}{3}=\frac{1}{6}$
$-(0,5+x)=\frac{1}{3}+\frac{1}{6}=\frac{1}{2}$
$0,5+x=\frac{-1}{2}$
$x=\frac{-1}{2}-0,5=-1$
b.
$(x+\frac{4}{9})(x-\frac{11}{5})=0$
$\Rightarrow x+\frac{4}{9}=0$ hoặc $x-\frac{11}{5}=0$
$\Rightarrow x=\frac{-4}{9}$ hoặc $x=\frac{11}{5}$
c.
$\frac{1}{3}-|\frac{5}{4}-2x|=\frac{1}{4}$
$|\frac{5}{4}-2x|=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}$
$\Rightarrow \frac{5}{4}-2x=\frac{1}{12}$ hoặc $\frac{5}{4}-2x=\frac{-1}{12}$
$\Rightarrow x=\frac{1}{2}(\frac{5}{4}-\frac{1}{12})$ hoặc $x=\frac{1}{2}(\frac{5}{4}+\frac{1}{12})$
$\Rightarrow x=\frac{7}{12}$ hoặc $x=\frac{2}{3}$
Đúng 0
Bình luận (0)
Thực hiện phép tính
2^16 x ( -9)^3 / ( -6)^5 x 16^
Mọi người giúp mik với ;-;
2^16x(-9)^3/(-6)^5x16=98304
nếu ko đúng thì cho mình xin lỗi nhé!
Cho 2 số thực x,y thỏa mãn: 0<x,y<=1 và x+y=3xy. Tìm GTNN và GTLN của P=x2+y2-4xy
Mọi người giúp mình nhé!
Câu 1: Phân tích đa thức thành nhân tử
a. 6x² - 3xy
b. x2 -y2 - 6x + 9
c. x2 + 5x - 6
Câu 2 thực hiện phép tính
a. x + 2² - x - 3 (x + 1)
b. x³ - 2x² + 5x - 10 : ( x - 2)
Câu 3 Cho biểu thức A (x - 5) / (x - 4) và B (x + 5)/ 2x - (x - 6) / (5 - x) - (2x² - 2x - 50) / (2x² - 10x) (điều kiện x khác 0, x khác 4, x khác 5
a. Tính giá trị của A khi x² - 3x 0
b. Rút gọn B
c. Tìm giá trị nguyên của x để A : B có giá trị nguyên
Câu 4: Cho tam giác ABC cân tại A đường cao AD, O là trung đi...
Đọc tiếp
Câu 1: Phân tích đa thức thành nhân tử
a. 6x² - 3xy
b. x2 -y2 - 6x + 9
c. x2 + 5x - 6
Câu 2 thực hiện phép tính
a. x + 2² - x - 3 (x + 1)
b. x³ - 2x² + 5x - 10 : ( x - 2)
Câu 3 Cho biểu thức A = (x - 5) / (x - 4) và B = (x + 5)/ 2x - (x - 6) / (5 - x) - (2x² - 2x - 50) / (2x² - 10x) (điều kiện x khác 0, x khác 4, x khác 5
a. Tính giá trị của A khi x² - 3x = 0
b. Rút gọn B
c. Tìm giá trị nguyên của x để A : B có giá trị nguyên
Câu 4: Cho tam giác ABC cân tại A đường cao AD, O là trung điểm của AC, điểm E đối xứng với điểm D qua cạnh OA.
a. Chứng minh tứ giác ADCE là hình chữ nhật
b. Gọi I là trung điểm của AD, chứng tỏ I là trung điểm của BE
c. cho AB = 10 cm BC = 12 cm. Tính diện tích tam giác OAB
cíu tớ với
1.Thực hiện phép tính:
a) 5xy2- x2y / 3xy + 4x2y + x2y / 3xy
Thực hiện phép tính:a) ( 5x4 – 3x3 + x2 ):3x2 b) ( 5xy2 + 9xy – x2 y2) : ( -xy)c) (x^3y^3-dfrac{1}{2}x^2y^3-x^3y^2) :dfrac{1}{3}x^2y^2 d)left(x^3-2x^2y+3xy^2right):left(-dfrac{1}{2}xright) e) (30x4y3 - 20x2y3 + 6x4y4) : 5x2y3
Đọc tiếp
Thực hiện phép tính:
a) ( 5x4 – 3x3 + x2 ):3x2 b) ( 5xy2 + 9xy – x2 y2) : ( -xy)
c) (\(x^3y^3-\dfrac{1}{2}x^2y^3-x^3y^2\)) :\(\dfrac{1}{3}x^2y^2\) d)\(\left(x^3-2x^2y+3xy^2\right):\left(-\dfrac{1}{2}x\right)\)
e) (30x4y3 - 20x2y3 + 6x4y4) : 5x2y3
a: \(=\dfrac{5}{3}x^2-x+\dfrac{1}{3}\)
b: \(=-5y-9+xy\)
Đúng 0
Bình luận (0)
thực hiện phép tính sau\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
MTC = (x - y)(x2 + xy + y2)
\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
\(=\dfrac{x^2+xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{3xy}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x^2-4xy+2y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
Đúng 1
Bình luận (0)
1/x-y-3xy/x^3-y^3+x-y/x^2+xy+y^2
=1/x-y+-3xy/(x-y)(x^2+xy+y^2)+x-y/x^2+xy+y^2
=x^2+xy+y^2/(x-y)(x^2+xy+y^2)+-3xy/(x-y)(x^2+xy+y^2)+x^2-2xy+y^2/(x-y)(x^2+xy+y^2)
=x^2+xy+y^2-3xy+x^2-2xy-y^2/(x-y)(x^2+xy+y^2)
=2x^2-5xy/(x-y)(x^2+xy+y^2)
Đúng 0
Bình luận (0)
MTC = (x - y)(x2 + xy + y2)
\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
\(=\dfrac{x^2+xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{3xy}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x^2-4xy+2y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
Đúng 0
Bình luận (0)
a) cho hai đa thức: A = x^2+5xy—3y^2; B=2x^2—3xy+11y^2.tính A+B b) thực hiện phép tính chia (9x^3y^2—12x^2y+15xy) : (3xy)
`#3107.101107`
a)
`A + B =` \(x^2+5xy-3y^2\)\(+ 2x^2-3xy+11y^2\)
`= (x^2 + 2x^2) + (5xy - 3xy) + (-3y^2 + 11y^2)`
`= 3x^2 + 2xy + 8y^2`
b)
\((9x^3y^2-12x^2y+15xy) \div (3xy)\)
`= 9x^3y^2 \div 3xy - 12x^2y \div 3xy + 15xy \div 3xy`
`= 3x^2y - 4x + 5`
Đúng 1
Bình luận (0)