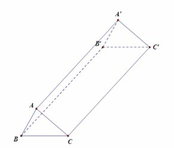
Cho hình lăng trụ đứng ABC. A’B’C’ (hình vẽ) có B A C ⏜ = 90 0 , AB = 6 cm, AC = 8 cm, AA’ = 15 cm. Diện tích toàn phần của hình lăng trụ đứng bằng
A. 258 c m 2
B. 360 c m 2
C. 456 c m 2
D. 408 c m 2
Cho lăng trụ đứng ABC. A’B’C’ có tất cả các cạnh bằng a và có G, G' lần lượt là trọng tâm của hai tam giác ABC và A’B’C’ (tham khảo hình vẽ).
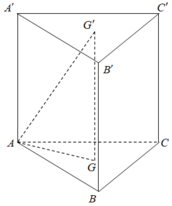
Thiết diện tạo bởi mặt phẳng (AGG') với hình lăng trụ đã cho là
A. Tam giác vuông
B. Tam giác cân
C. Hình vuông
D. Hình chữ nhật
Chọn D
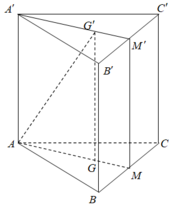
Gọi M, M' lần lượt là trung điểm của BC và B’C’. Khi đó thiết diện của lăng trụ tạo bởi mặt phẳng (AGG') là hình chữ nhật AMM'A’.
Mà A M ’ = a . s i n 60 0 = a 3 2 ≠ A A ’
Nên AMM’A’ không thể là hình vuông.
Cho hình lăng trụ đứng ABC. A’B’C’ có tam giác ABC vuông tại A, AB= AA’=a, AC =2a . Tính thể tích khối lăng trụ đã cho
A. a 3 3
B. 2 a 3 3
C. a 3
D. 2 a 3
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy là tam giác vuông cân tại đỉnh A, mặt bên BCC’B’ là hình vuông, khoảng cách giữa AB’ và CC’ bằng a. Thể tích của khối trụ ABC. A’B’C’.
A. a 3
B. 2 a 3 2
C. 2 a 3 3
D. 2 a 3
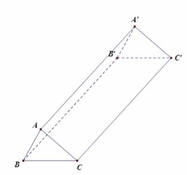
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy tam giác ABC vuông tại A, AB = 6 cm, AC = 8 cm, AA’ = 12 cm. Diện tích toàn phần của hình lăng trụ đó bằng
A. 288 c m 2
B. 360 c m 2
C. 456 c m 2
D. 336 c m 2


Diện tích toàn phần là:
S t p = 288 + 2 . 24 = 336 c m 2
Đáp án cần chọn là D
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông cân tại C với CA = CB = a. Trên đường chéo CA' lấy hai điểm M, N. Trên đường chéo AB' lấy được hai điểm P, Q sao cho MPNQ tạo thành một tứ diện đều. Tính thể tích khối lăng trụ ABC. A’B’C’
A. 2 a 3
B. a 3 6
C. a 3
D. a 3 2
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A’B’C’) bằng a 6 . Thể tích của khối lăng trụ bằng
A. 3 2 a 3 4
B. 3 2 a 3 8
C. 3 2 a 3 28
D. 3 2 a 3 16
Chọn đáp án D
Gọi M là trung điểm của BC. Suy ra
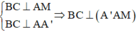
![]()
![]()
![]()
Ta có
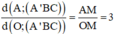
![]()
∆ A ' A M vuông tại A, AH là đường cao nên
![]()
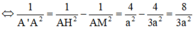
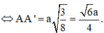
Thể tích khối lăng trụ là: V A B C . A ' B ' C ' = 3 2 a 3 16
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B, AB = BC = a, BB’ = a 3 Tính góc giữa đường thẳng A’B và mặt phẳng (BCC’B’)
A. 45 0
B. 30 0
C. 60 0
D. 90 0
43:cho hình lăng trụ đứng ABC.EFD có góc ABC=90 độ,CD=6cm,BC=4cm,S tứ giác AEDC=30cm2.
a)Tính AB
b)Tính Stp và V của hình lăng trụ đứng ABC.EFD
44:Hình lăng trụ đứng ABC.A'B'C' có thể tích 56cm3,chiều cao 7cm và đáy là tam giác vuông có 1 cạnh góc vuông là 5cm.Vẽ hình và tính các cạnh còn lại của đáy hình lăng trụ này.
Cho lăng trụ đứng tam giác ABC.A'B'C' như hình vẽ a, có đáy là tam giác ABC vuông cân tại B và AC = 5 cm, BB' = 7 cm.
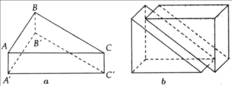
a) Tính diện tích toàn phần của lăng trụ ABC.A’B'C'.
b) Ghép 2 hình lăng trụ đứng có cùng kích thước như lăng trụ đứng ABC.A'B'C' (như hình b). Tính thể tích của hình lăng trụ đứng mới được tạo thành.