Cho hình lăng trụ đứng ABC. A’B’C’ có AB = 5 cm, AC = 12 cm, BC = 13 cm. Mặt phẳng nào dưới đây không vuông góc với mặt phẳng (ABB’A’)?
A. (BCC’B’)
B. (ABC)
C. (A’B’C’)
D. (ACC’A’)
Cho hình lăng trụ A B C . A ' B ' C ' có A B = 1 , A C = 2 , ∠ C A B = 135 0 , A A ' = 1 . Hình chiếu vuông góc của điểm A trên mặt phẳng (A’B’C’) trùng với trung điểm H của B’C’, Số đo của góc hợp bởi đường thẳng AH và mặt phẳng (ABB’A’) bằng
A. 30 0
B. 60 0
C. 45 0
D. 90 0
Cho hình lăng trụ ABC.A'B'C' có A B = 1 , A C = 2 , C A B ^ = 135 0 , A A ' = 1 . Hình chiếu vuông góc của điểm A trên mặt phẳng (A’B’C’) trùng với trung điểm H của B’C’, Số đo của góc hợp bởi đường thẳng AH và mặt phẳng (ABB’A’) bằng
Cho hình lăng trụ đứng tam giác ABC. A’B’C’, có cạnh bên AA’ = 21 cm, tam giác ABC vuông cân tại A, BC = 42 cm. Tính khoảng cách từ A đến mặt phẳng (A’BC).
A. 21 2 c m
B. 21 2 2 c m
C. 21 2 c m
D. 21 2 4 c m
Chọn B.
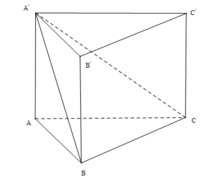
- Tam giác ABC vuông cân tại A, BC = 42cm
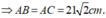
- Tứ diện A.A’BC là tứ diện vuông tại A. Gọi h = d( A, (A’BC)), ta có:
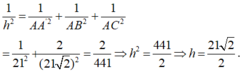
Cho hình lăng trụ đứng ABCD.A'B'C'D' có hai đáy là các hình vuông tâm O và tâm O', AB = 5 cm và AC ’ = 15 cm.
a) Hình lăng trụ đứng đã cho có phải hình lập phương không? Vì sao?
b) Chứng minh đường thẳng OO' vuông góc vói mặt phẳng (ABCD).
c) Tìm giao tuyến của hai mặt phẳng (ACC'A') và (BDD'B’).
d) Tính chiều cao của hình lăng trụ đứng
a) Không vì AA' ≠ AB.
b) HS tự chứng minh.
c) Giao tuyến là OO'.
d) Chiều cao là 5 7 c m
Cho hình lăng trụ đứng ABC.A'B'C' có AB = 5cm, AC = 12cm,BC = 13cm. Có bao nhiêu mặt phẳng vuông góc với mặt phẳng ( ABB'A' ) ?
A. 1
B. 2
C. 4
D. 3
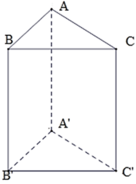
Ta có: A B 2 + A C 2 = B C 2 ⇒ Δ ABC vuông tại A.
Do đó: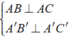
Vì AC vuông góc với hai đường thẳng cắt nhau là AB và AA'
Nên AC ⊥ ( ABB'A' )
Vậy có 3 mặt phẳng vuông góc với ( ABB'A' ) là:
( ABC ), ( A'B'C' ),( ACC'A' )
Chọn đáp án D.
Cho lăng trụ ABC.A’B’C’có AB=2a, A B C ⏜ = 120 0 , BC=2a, Hình chiếu vuông góc của A trên mặt phẳng (A’B’C’) trung với điểm của A’B’. Góc giữa đường thẳng AC’ và mặt phẳng (A’B’C’) bằng 60 0 . Gọi α là góc giữa hai mặt phẳng (BCC’B’) và (ABC). Khi đó, tan α có giá trị là:
A. 21
B. 2 2
C. 21 2
D. 2 21
Cho lăng trụ ABC.A’B’C’có AB = 2a, BC = 2a, góc A’B’C’ = 120 0 . Hình chiếu vuông góc của A trên mặt phẳng (A’B’C’) trung với điểm của A’B’. Góc giữa đường thẳng AC’ và mặt phẳng (A’B’C’) bằng 60 0 . Gọi α là góc giữa hai mặt phẳng (BCC’B’) và (ABC). Khi đó, tan α có giá trị là:
A. 21
B. 2 2
C. 21 2
D. 2 21
Đáp án D
Phương pháp: Cho hai mặt phẳng (α) và (β) cắt nhau, ta xác định góc giữa (α) và (β) như sau:
- Tìm giao tuyến ∆ của hai mặt phẳng (α) và (β).
- Tìm trong mỗi mặt phẳng (α), (β) một đường thẳng 𝑎, cùng cùng vuông góc với ∆ và cùng cắt ∆ tại điểm .
- Xác định góc giữa 𝑎 và 𝑏.
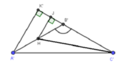
Cách giải: Gọi H là trung điểm của A’B’ => AH ⊥ (A’B’C’)
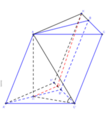
Kẻ HJ, A'K' ⊥ B'C', (J, K' ∈ B'C'), AK ⊥ BC, (K ∈ BC)
HJ//A'K', A'K'//AK => HJ//AK => H,J,A,K đồng phẳng
Vì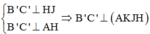 
Ta có: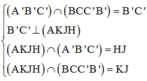 
=> ((BCC'B');(A'B'C')) = (KJ;HJ)
A ' B ' K ' ^ = 180 0 - 120 0 = 60 0
=> A'K' = A'B' . sin 60 0
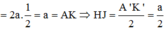
Xét ∆B’HC’ : H'C = 
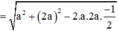
∆AHC’ vuông tại H => AH = HC.tanC’ = HC.tan(AC’;(A’B’C’)) (vì AH ⊥ (A’B’C’))
Xét hình thang vuông AKJH:
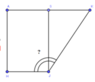
Kẻ 
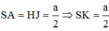
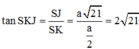
Vì AK//HJ
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B, AB = BC = a, BB’ = a 3 Tính góc giữa đường thẳng A’B và mặt phẳng (BCC’B’)
A. 45 0
B. 30 0
C. 60 0
D. 90 0
