Tính diện tích toàn phần hình chóp tứ giác đều dưới đây
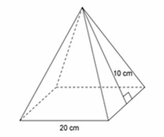
A. 600 c m 2
B. 700 c m 2
C. 800 c m 2
D. 900 c m 2
Bài 26) Một hình chóp tứ giác đều có chiều cao 6cm, cạnh đây 5cm. a Tính diện tích toàn phần của hình chóp? b/ Tinh thể tích của hình chóp
Lời giải:
a. Diện tích đáy: $5.5=25$ (cm2)
Chiều cao mỗi hình mặt bên: $\sqrt{6^2+(5:2)^2}=6,5$ (cm)
Diện tích mỗi mặt bên: $6,5.5:2=16,25$ (cm2)
Diện tích toàn phần: $25+16,25=41,25$ (cm2)
b. Thể tích: $\frac{1}{3}.6.25=50$ (cm3)
Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều cạnh đáỵ 1m, chiều cao hình chóp 50cm
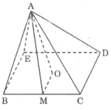
Hình chóp tứ giác đều, cạnh đáy bằng 1m, chiếu cao hình chóp bằng 0,5m.
Tương tự hình vẽ câu a ta có AM Δ BC.
Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.
Áp dụng định li Pi-ta-go vào tam giác vuông AOM,ta có:
A M 2 = O A 2 + O M 2 = 0 , 5 2 + 0 , 5 2 = 0 , 5
Suy ra: AM = 0,5 cm
Ta có: S x q =1.2. 0 , 5 =2 0 , 5 ( m 2 )
S đ á y = 1.1=1( m 2 )
Vậy S T P = S x q + S đ á y = 2 0 , 5 + 1 ≈ 2,4( m 2 )
Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều cạnh đáỵ 20cm, chiều cao hình chóp 7cm
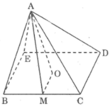
Hình chóp tứ giác đều, cạnh đáy bằng 20cm, chiều cao hình chóp bằng 7cm
Tương tự hình vẽ câu a ta có MA Δ BC
Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = O A 2 + O M 2 = 49 + 100 = 149
Suy ra: AM = 149 cm
Ta có: S x q =20.2. 149 =40 149 ( c m 2 )
S đ á y = 20.20= 400( c m 2 )
Vậy S T P = S x q + S đ á y = 40 149 +400 ≈ 888,3( c m 2 )
Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều OA = 8cm,BC = CD = 6cm
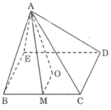
Vì AO là đường cao hình chóp nên ΔAOM vuông tại O.
Ta có OM = 1/2 CD = 3 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = A O 2 + O M 2 = 8 2 + 3 2 = 73
Suy ra: AM = 73 (cm)
Ta có: S x q = Pd = 6.2. 73 = 12 73 ( c m 2 )
S đ á y = 6.6 = 36 ( c m 2 )
Vậy S T P = S x q + S đ á y = 12√73 +36 ≈ 138,5( c m 2 )
Tính diện tích toàn phần của các hình chóp đều sau đây :
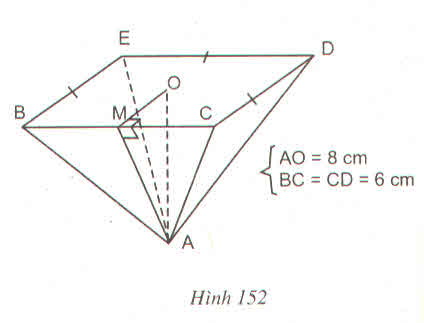
a) Hình cho theo các kích thước trên hình 152
b) Hình chóp tứ giác đều, cạnh đáy 6cm, chiều cao hình chóp 5cm
c) Hình chóp tứ giác đều, cạnh đáy 20cm, chiều cao hình chóp 7cm
d) Hình chóp tứ giác đều, cạnh đáy 1m, chiều cao hình chóp 50cm
Cho hình chóp tam giác đều SABC gọi M là tr/đ của AB.Bt SM=5cm,SA=căn 29
a)Tính cạnh đáy của hình chóp b)tính diện tích xung quanh của hình chóp c)tính diện tích toàn phần của hình chópa: S.ABC là hình chóp đều
=>SA=SB=SC và AB=AC=BC
ΔSAB cân tại S có SM là trung tuyến
nên SM vuông góc AB
=>ΔSMA vuông tại M
\(MA=\sqrt{SA^2-SM^2}=2\left(cm\right)\)
=>BA=2*2=4cm=BC=AC
b: \(S_{Xq}=\dfrac{1}{2}\left(4+4+4\right)\cdot5=6\cdot5=30\left(cm^2\right)\)
c: \(S_{tp}=30+4^2\cdot\dfrac{\sqrt{3}}{4}=30+4\sqrt{3}\left(cm^2\right)\)
Hình chóp tam giác đều có diện tích đáy là \(30\) \(c{m^2}\), mỗi mặt bên có diện tích \(42\) \(c{m^2}\), có diện tích toàn phần là:
A. \(126c{m^2}\) B. \(132c{m^2}\) C. \(90c{m^2}\)
Diện tích toàn phần: `42 xx 3 + 30 = 152 cm^2.`
`=> D`.
Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đếu cạnh đáy 6cm, chiều cao hình chóp 5cm.
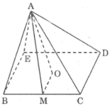
Hình chóp tứ giác đều cạnh đáy bằng 6cm, chiều cao hình chóp bằng 5cm.
Tương tự hình vẽ câu a ta có MA Δ BC.
Vì AO là đường cao của hình chóp nên △ AOM vuông tại O.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = O A 2 + O M 2 = 25 + 9 = 34
Suy ra: AM = 34 cm
Ta có: S x q =6.2. 34 =12 34 ( c m 2 )
S đ á y = 6.6 = 36 ( c m 2 )
Vậy S T P = S x q + S đ á y = 12 34 +36 ≈ 106 ( c m 2 )
Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây (h.126).
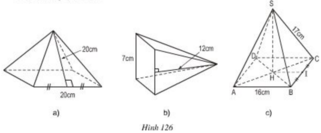
Diện tích xung quanh:
Hình a:
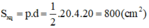
(trong đó chu vi đáy là 20.4 cm)
Diện tích đáy: Sd = 202 = 400 (cm2)
Diện tích toàn phần: Stp = Sxq + Sđ = 800 + 400 = 1200 (cm2)
Hình b:
Chu vi đáy là 4.7 = 28 (cm)
Diện tích xung quanh là:
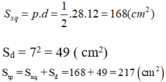
Hình c:
+) Diện tích đáy là Sd= 162 = 256 (cm2 ).
Do I là trung điểm của BC nên
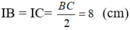
+) Tam giác SBC có SI là đường trung tuyến nên đồng thời là đường cao.
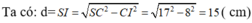
+) Chu vi đáy là: 16 .4 = 64 (cm)
+) Diện tích xung quanh là:
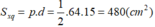
+) Diện tích toàn phần là:
Stp = Sđ + Sxq = 256 + 480 = 736 (cm2).