Cho hình thang cân MNPQ (MN // PQ) có góc M Q P ^ = 45 ° và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:
A. 728 c m 2 .
B. 346 c m 2 .
C. 364 c m 2 .
D. 362 c m 2 .
Cho hình thang cân MNPQ (MN // PQ) có góc M Q P ^ = 45 ° và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:
A. 418 c m 2 .
B. 209 c m 2
C. 290 c m 2 .
D. 580 c m 2 .
Đáp án cần chọn là: B
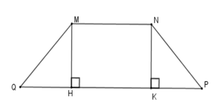
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 8 cm nên QH = KP = 30 − 8 2 = 8 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 8 + 30 ) .11 2 = 209 c m 2 .
cho hình thang cân MNPQ có độ dài cạnh đáy là MN = 7cm, độ dài cạnh đáy PQ gấp đôi độ dài cạnh đáy MN , độ dài chiều cao MH= 4cm.Tính diện tích hình thang cân ABCD?
PQ=7*2=14cm
\(S_{MNPQ}=\dfrac{1}{2}\cdot\left(7+14\right)\cdot4=2\cdot21=42\left(cm^2\right)\)
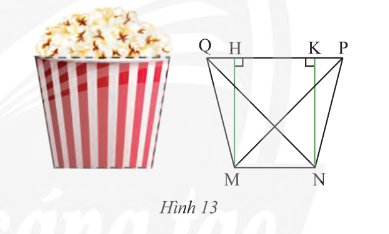
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân \(MNPQ\) (Hình 13) với hai đáy \(MN = 6cm\), \(PQ = 10\)cm và độ dài hai đường chéo \(MN = NQ = 8\sqrt 2 \) cm. Tính độ dài đường chéo và cạnh bên của hình thang
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
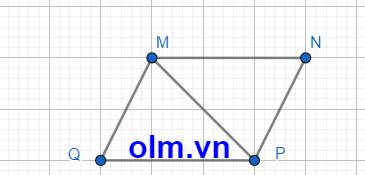
Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
\(\widehat{QPM}\) = \(\widehat{PMN}\) (2 góc so le trong)
\(\widehat{QMP}\) = \(\widehat{NPM}\) (2 góc so le trong)
\(\Rightarrow\) \(\Delta\)MPQ = \(\Delta\)PMN (g-c-g)
\(\Rightarrow\) PQ = MN; MQ = PN (đpcm)
b, Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
MN = PQ
\(\widehat{QPM}\) = \(\widehat{PMN}\) ( 2 góc so le trong)
⇒\(\Delta\)MPQ = \(\Delta\)PMN ( cạnh góc cạnh)
\(\Rightarrow\) MQ = NP (đpcm)
⇒ \(\widehat{QMP}\) = \(\widehat{NPM}\)
Mà hai góc \(\widehat{QMP}\) và \(\widehat{NPM}\) ở vị trí so le trong và bằng nhau nên:
QM // NP (đpcm)
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
bài 1 :
a) Ta có MQ//NP (theo giả thiết).
Chứng minh MN = PQ:
Vì MN//PQ và MQ//NP, ta có hai tam giác MNP và QMQ' đồng dạng (theo nguyên lý đồng dạng của tam giác có hai cặp góc tương đồng bằng nhau).
Do đó, ta có tỉ số đồng dạng giữa các cạnh của hai tam giác là:
MN/MQ = NP/QM
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MN/MQ = NP/NP
Từ đó suy ra: MN = PQ.
Chứng minh MQ = NP:
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MQ/MN = NP/PQ
Vì MN = PQ (đã chứng minh ở trên), nên ta có tỉ số đồng dạng:
MQ/MN = NP/NP
Từ đó suy ra: MQ = NP.
b) Ta có MN = PQ (theo giả thiết).
Chứng minh MQ//NP:
Giả sử MQ không // NP. Khi đó, MQ và NP sẽ cắt nhau tại một điểm O.
Vì MN//PQ và MQ//NP, nên ta có hai tam giác MNP và QMQ' đồng dạng (theo nguyên lý đồng dạng của tam giác có hai cặp góc tương đồng bằng nhau).
Do đó, ta có tỉ số đồng dạng giữa các cạnh của hai tam giác là:
MN/MQ = NP/QM
Từ đó suy ra: MN/MQ = NP/NP
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MN/MQ = NP/NP
Từ đó suy ra: MN = PQ.
Điều này mâu thuẫn với giả thiết MN = PQ (đã cho). Vậy giả sử MQ không // NP là sai.
Do đó, ta kết luận rằng MQ//NP.
Chứng minh MQ = NP:
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MQ/MN = NP/PQ
Vì MN = PQ (đã chứng minh ở trên), nên ta có tỉ số đồng dạng:
MQ/MN = NP/NP
Từ đó suy ra: MQ = NP.
bài 2 :
a) Ta có MN = MQ và góc M = 50 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc N = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
50 độ + góc N + 90 độ + góc N = 360 độ
Simplifying the equation:
140 độ + 2góc N = 360 độ
Trừ 140 độ từ hai phía:
2góc N = 220 độ
Chia cho 2:
góc N = 110 độ
Vậy số đo góc MQN là 110 độ.
b) Ta đã biết góc P = 90 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc M = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
góc M + 110 độ + 90 độ + góc M = 360 độ
Simplifying the equation:
2góc M + 200 độ = 360 độ
Trừ 200 độ từ hai phía:
2góc M = 160 độ
Chia cho 2:
góc M = 80 độ
Vậy số đo góc MQP là 80 độ.
c) Để chứng minh MP vuông góc với NQ, ta cần chứng minh rằng góc MPN + góc NQP = 90 độ.
Ta đã biết góc P = 90 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc M = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
góc M + góc N + 90 độ + góc M = 360 độ
Simplifying the equation:
2góc M + góc N = 270 độ
Vì góc M = góc Q, nên ta có:
2góc M + góc M = 270 độ
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
Cho hình thang cân MNPQ ( MN//PQ , MN < PQ ), NP=15cm, đường cao NI = 12cm, QI= 16cm
a)Tính độ dài IP, MN
b)Chứng minh rằng QN\(\perp\)NP
c)Tính diện tích hình thang MNPQ
d)Gọi E là trung điểm của PQ. Đường thẳng vuông góc với EN tại N cắt đường thẳng PQ tại K. Chứng minh \(KN^2=MP.KQ\)
Hình thang MNPQ (MN//PQ) có góc M-góc Q=40 độ và góc N chia cho góc P=4/5
Ta có: MN//PQ
nên \(\widehat{M}+\widehat{Q}=180^0\)
mà \(\widehat{M}-\widehat{Q}=40^0\)
nên \(2\cdot\widehat{M}=220^0\)
\(\Leftrightarrow\widehat{M}=110^0\)
\(\Leftrightarrow\widehat{Q}=70^0\)
Ta có: \(\widehat{N}+\widehat{P}=180^0\)
\(\Leftrightarrow\widehat{P}\cdot\dfrac{9}{5}=180^0\)
\(\Leftrightarrow\widehat{P}=100^0\)
\(\Leftrightarrow\widehat{N}=80^0\)