Cho đường tròn O, đường kính AB. Lấy C thuộc (O) (C khác A và B). Tiếp tuyến tại A của đường tròn O cắt BC tại M. a, CM: tam giác ABC vuông và BA2=BC.BM b, Gọi K là trung điểm của MA. CM:KC là tiếp tuyến của đường tròn O

Những câu hỏi liên quan
Cho đường tròn O, đường kính AB. Lấy C thuộc (O) (C khác A và B). Tiếp tuyến tại A của đường tròn O cắt BC tại M.
a, CM: tam giác ABC vuông và BA2=BC.BM b, Gọi K là trung điểm của MA. CM:KC là tiếp tuyến của đường tròn O
a: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔBAM vuông tại A có AC là đường cao ứng với cạnh huyền MB
nên \(BA^2=BC\cdot BM\)
Đúng 4
Bình luận (0)
Cho đường tròn (O) đường kính AB và dây AC không đi qua O (AC<AB).Gọi I là trung điểm AC.
a)Chứng minh OI//BC
b)Tiếp tuyến tại C của đường tròn (O) cắt tia OI ở M
CM: MA là tiếp tuyến
c)BM cắt đường cao CH của tam giác ABC tại K, và N là giao giao điểm tia BC và tia AM. CM:KC=KH
Giải giúp mình các bài này với ạ!1) Từ điểm A nằm ngoài đường tròn tâm O, vẽ tiếp tuyến AB (B là tiếp điểm). Lấy điểm C thuộc đường tròn tâm (O) khác điểm B sao cho AB ACa. CM : Tam giác OAB tam giác OACb. CM : AC là tiếp tuyến của đường tròn tâm Oc. Gọi I là giao điểm của OA và BC. Tính AB biết bán kính (R) 5cm, BC 8cm2) Lấy 2 điểm A và B thuộc đường tròn tâm O (3 điểm A, B, O không thẳng hàng). Tiếp tuyến của O tại A cắt tia phân giác của góc AOB tại C.a. So sánh tam giác OAC và tam giác O...
Đọc tiếp
Giải giúp mình các bài này với ạ!
1) Từ điểm A nằm ngoài đường tròn tâm O, vẽ tiếp tuyến AB (B là tiếp điểm). Lấy điểm C thuộc đường tròn tâm (O) khác điểm B sao cho AB = AC
a. CM : Tam giác OAB = tam giác OAC
b. CM : AC là tiếp tuyến của đường tròn tâm O
c. Gọi I là giao điểm của OA và BC. Tính AB biết bán kính (R) = 5cm, BC = 8cm
2) Lấy 2 điểm A và B thuộc đường tròn tâm O (3 điểm A, B, O không thẳng hàng). Tiếp tuyến của O tại A cắt tia phân giác của góc AOB tại C.
a. So sánh tam giác OAC và tam giác OBC.
b. CM : BC là tiếp tuyến của đường tròn tâm O
3) Cho đường tròn tâm O, bán kính R. Lấy điểm A cách O một khoảng = 2R. Từ A vẽ 2 tiếp tuyến AB, AC (B,C là tiếp điểm). OA cắt đường tròn tâm O tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a. CM : OK // AB
b. CM : tam giác OAK là tam giác cân
c. CM : KI là tiếp tuyến của đường tròn tâm O.
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là t...
Đọc tiếp
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB
3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là trung điểm CH,BM cắt tiếp tuyến Ax của O tại P .chứng minh PC là tiếp tuyến của (O)
4.cho đường tròn O đường kính AB, M là một điểm trên OB.đường thẳng qua M vuông góc với AB tại M cắt O tại C và D. AC cắt BD tại P,AD cắt BC tại Q,AB cắt PQ tai I chứng minh IC,ID là tiếp tuyến của (O)
5.cho tam giác ABC nội tiếp đường tròn đường kính BC (AB<AC).T là một điểm thuộc OC.đường thẳng qua T vuông góc với BC cắt AC tại H và cắt tiếp tuyến tại A của O tại P.BH cắt (O) tại D. chứng minh PD là tiếp tuyến của O
6.cho tam giác ABC nội tiếp đường tròn O. phân giác góc BAC cắt BC tại D và cắt (O) tại M chứng minh BM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD
Cho đường tròn (O;R) đường kính AB và điểm C thuộc đường tròn (O) (C khác A, B). Kẻ CH ⊥ AB tại H.a) Cm: ∆ABC vuông và CH² AC × BC × sin A × cos Ab) Tiếp tuyến tại A của đường tròn (O) cắt tia BC ở D. Gọi I là trung điểm AD. C/m IC là tiếp tuyến của (O).c) Tiếp tuyến tại B của đường tròn (O) cắt IC ở K. Cm IA × BK R²d) Xác định vị trí của điểm C trên đường tròn (O) để diện tích tứ giác ABKI nhỏ nhất.
Đọc tiếp
Cho đường tròn (O;R) đường kính AB và điểm C thuộc đường tròn (O) (C khác A, B). Kẻ CH ⊥ AB tại H.
a) Cm: ∆ABC vuông và CH² = AC × BC × sin A × cos A
b) Tiếp tuyến tại A của đường tròn (O) cắt tia BC ở D. Gọi I là trung điểm AD. C/m IC là tiếp tuyến của (O).
c) Tiếp tuyến tại B của đường tròn (O) cắt IC ở K. Cm IA × BK = R²
d) Xác định vị trí của điểm C trên đường tròn (O) để diện tích tứ giác ABKI nhỏ nhất.
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
Xét ΔCHA vuông tại H có \(sinA=\dfrac{CH}{CA}\)
=>\(CH=CA\cdot sinA\)
Xét ΔCHB vuông tại H có \(sinB=\dfrac{CH}{CB}\)
=>\(CH=CB\cdot sinB\)
=>\(CH=CB\cdot cosA\)
\(CA\cdot CB\cdot sinA\cdot cosA\)
\(=CH\cdot CH=CH^2\)
b: ΔACD vuông tại C
mà CI là đường trung tuyến
nên IA=IC=ID
Xét ΔIAO và ΔICO có
IA=IC
AO=CO
IO chung
Do đó: ΔIAO=ΔICO
=>\(\widehat{ICO}=\widehat{IAO}=90^0\)
=>IC là tiếp tuyến của (O)
c: ΔIAO=ΔICO
=>\(\widehat{AOI}=\widehat{COI}\)
=>\(\widehat{AOC}=2\cdot\widehat{IOC}\)
Xét (O) có
KB,KC là tiếp tuyến
Do đó: KB=KC và OK là phân giác của góc COB
=>\(\widehat{COB}=2\cdot\widehat{COK}\)
\(\widehat{AOC}+\widehat{COB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{IOC}+2\cdot\widehat{COK}=180^0\)
=>\(\widehat{IOC}+\widehat{COK}=90^0\)
=>\(\widehat{IOK}=90^0\)
Xét ΔIOK vuông tại O có OC là đường cao
nên \(CI\cdot CK=OC^2\)
=>\(AI\cdot BK=R^2\)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A (AB<AC). M là trung điểm AC. Đường tròn đường kính MC cắt BC tại N. BM kéo dài cắt đường tròn tại D
a)CM: A,B,C,D cùng thuộc 1 đường tròn
b) Gọi O là trung điểm BC, CM: OM là tiếp tuyến của đường kính MC
a) Tam giác ABC vuông tại A (gt).
=> A; B; C cùng thuộc đường tròn đường kính BC. (1)
Xét đường tròn đường kính MC:
D \(\in\) đường tròn đường kính MC (gt).
=> \(\widehat{MDC}=90^o\) hay \(\widehat{BDC}=90^o.\)
Tam giác BDC vuông tại D (\(\widehat{BDC}=90^o\)).
=> B; D; C cùng thuộc đường tròn đường kính BC. (2)
Từ (1); (2) => A; B; C; D cùng thuộc đường tròn đường kính BC.
b) Xét tam giác ABC có:
+ O là trung điểm BC (gt).
+ M là trung điểm AC (gt).
=> OM là đường trung bình.
=> OM // AB (Tính chất đường trung bình).
Mà AB \(\perp\) MC (AB \(\perp\) AC).
=> OM \(\perp\) MC.
Xét đường tròn đường kính MC: OM \(\perp\) MC (cmt); M \(\in\) đường tròn đường kính MC (gt).
=> OM là tiếp tuyến.
Đúng 1
Bình luận (0)
Cho đường tròn tâm O có đường kính AB.Vẽ điểm C thuộc đường tròn (O) (C khác A và B).Tiếp tuyến tại A cắt BC tại I.Gọi M là trung điểm IA. a)C/m: tam giác ABC vuông và OM vuông góc AC. b)C/m:MC là tiếp tuyến đường tròn tâm O. c)Tia MC cắt tiếp tuyến By của đường tròn (O) tại E.C/m đường cao CH của tam giác ABC và 2 đường thẳng MB,AE đồng quy tại 1 điểm
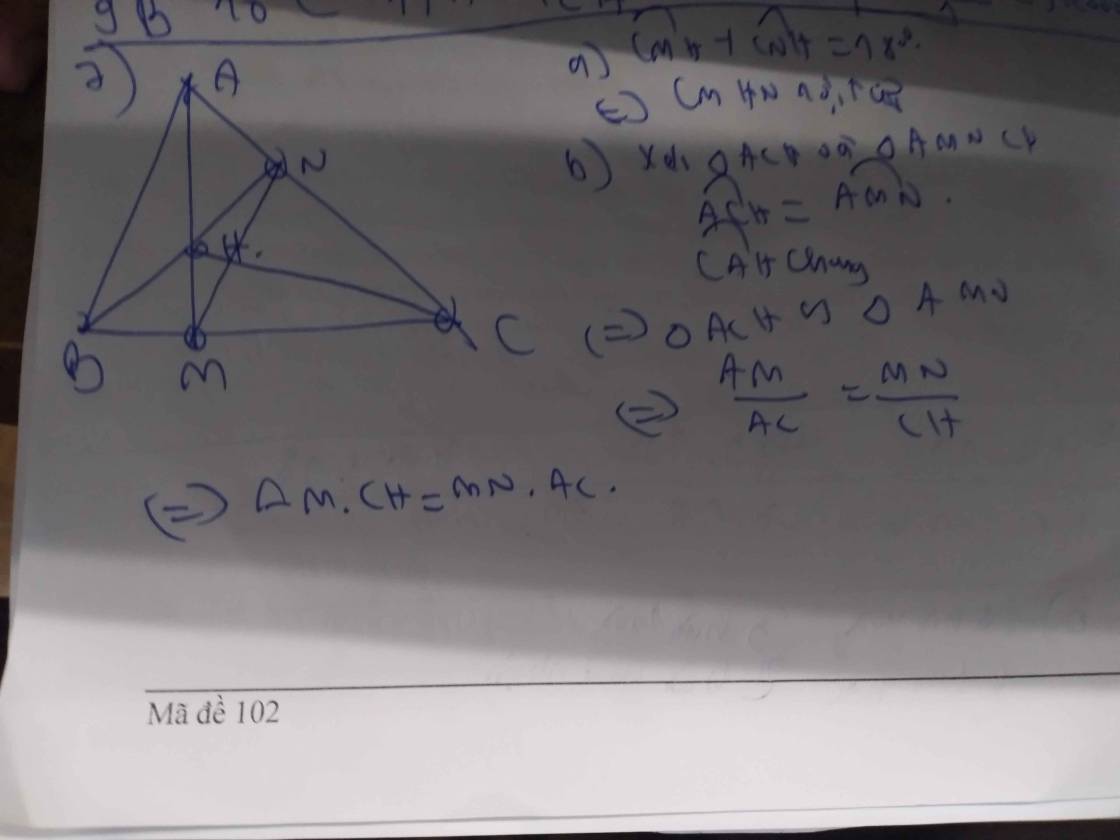
Bài 5:Cho tam giác ABC vuông tại A, có AB 8 cm; AC 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.a)Tính độ dài đoạn BC và AMb)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.c) Chứng minh tứ giác OACE nội tiếp Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (MBC, NAC). Hai đường cao AM và BN cắt nhau tại H.a)Chứng minh rằng tứ giác CMHN nội tiếp một đường trònb)Chứng minh rằng AM.CH AC.MN
Đọc tiếp
Bài 5:Cho tam giác ABC vuông tại A, có AB = 8 cm; AC = 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.
a)Tính độ dài đoạn BC và AM
b)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.
c) Chứng minh tứ giác OACE nội tiếp
Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (M=BC, N=AC). Hai đường cao AM và BN cắt nhau tại H.
a)Chứng minh rằng tứ giác CMHN nội tiếp một đường tròn
b)Chứng minh rằng AM.CH = AC.MN
Cho đường tròn O, đường kính AB. Lấy C thuộc (O) (C khác A và B). Tiếp tuyến tại A của đường tròn O cắt BC tại M.
a, CM: tam giác ABC vuông và BA2=BC.BM b, Gọi K là trung điểm của MA. CM:KC là tiếp tuyến của đường tròn O c, KC là tiếp tuyến tại B của đường tròn O tại D . CM: tam giác KOD vuông. d, xác định tâm của đường tròn O nội tiếp tam giác BCD