Cho hàm số f(x)= | 3 x 4 - 4 x 3 - 12 x 2 + m | . Gọi M là giá trị lớn nhất của hàm số trên đoạn [-1;3]. Giá trị nhỏ nhất của M bằng
A. 59 2
B. 5 2
C. 16
B. 57 2
Cho hàm số f(x)=| 3 x 4 - 4 x 3 - 12 x 2 + m |. Gọi M là giá trị lớn nhất của hàm số trên đoạn [-1;3]. Có bao nhiêu số thực m để M= 59 2 .
A. 2.
B. 6.
C. 1.
D. 4.
Cho hàm số f x = 3 x 4 - 4 x 3 - 12 x 2 + m Gọi M là giá trị lớn nhất của hàm số trên đoạn - 1 ; 3 Giá trị nhỏ nhất của M bằng
A. 59 2
B. 5 2
C. 16
D. 57 2
Cho hàm số y = f(x) = | x 4 - 4 x 3 + 4 x 2 + a |. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Số giá trị nguyên a thuộc đoạn [-3;3] sao cho M ≤ 2m là
A. 3
B. 5
C. 6
D. 7
Chọn B
Xét g(x) = x 4 - 4 x 3 + 4 x 2 + a với x ∈ [0;2]
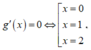
Bảng biến thiên g(x)
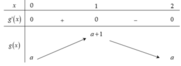
Trường hợp 1: a ≥ 0. Khi đó M = a + 1; m = a
Ta có M
≤
2m 
Với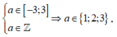 
Trường hợp 2: 
Khi đó M = -a; m = -(a+1)
Trường hợp 3: -1 < a < 0. Với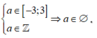 
Vậy có 5 giá trị a cần tìm.
Cho hàm số f(x) = | x 4 - 4 x 3 + 4 x 2 + a |. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;2] sao cho M ≤ 2m?
A. 7
B. 5
C. 6
D. 4
Chọn D
Xét hàm số f(x) = x 4 - 4 x 3 + 4 x 2 + a trên đoạn [0;2], ta có:
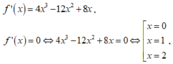
trên đoạn
Vì 
nên trên đoạn [0;2] giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
lần lượt là a+1, a
Suy ra 
nếu 
nếu 
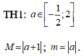
Khi đó 
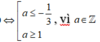
nên chọn 
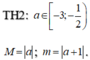
Khi đó 
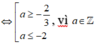nên chọn 
Vậy có 4 giá trị a thỏa yêu cầu
Cho hàm số y = f(x) nghịch biến trên ℝ và thỏa mãn [f(x) - x]f(x) = x 6 + 3 x 4 + 2 x 2 , ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng
A. 4
B. -28
C. -3
D. 33
Chọn A
Ta có: 
Với 
nên f(x) đồng biến trên
ℝ
Với 
nên f(x) nghich biến trên
ℝ
Suy ra: 
Vì f(x) nghich biến trên
ℝ
nên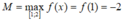 
và 
Từ đây ,ta suy ra: 
=> chọn đáp án A
Cho hàm số f ( x ) = x 4 - 4 x 3 + 4 x 2 + a . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0; 2] .Có bao nhiêu số nguyên a thuộc đoạn [-3; 3] sao cho M ≤ 2 m ?
A. 3
B. 7
C. 6
D. 5
Đáp án D
Xét hàm số 
.
;
Bảng biến thiên
Do 
nên 
suy ra 
.
Suy ra 
.
Nếu 
thì 
, 
.
Nếu 
thì 
, 
.
Do đó 
hoặc 
, do a nguyên và thuộc đoạn 
nên 
.
Tập hợp các giá trị của m để hàm số y = | 3 x 4 - 4 x 3 - 12 x 2 + m - 1 | có điểm cực trị là:
A. (0;6)
B. (6;33)
C. (1;33)
D. (1;6)
Chọn D
Xét hàm số f(x) = 3 x 4 - 4 x 3 - 12 x 2 + m - 1
Có 
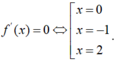
Bảng biến thiên:
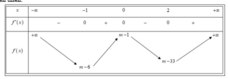
Từ bảng biến thiên, ta có hàm số y = |f(x)| có T điểm cực trị ⇔ đồ thị hàm số y = f(x) cắt Ox tại điểm phân biệt
Tập hợp các giá trị của m để hàm số y = 3 x 4 - 4 x 3 - 12 x 2 + m - 1 có T điểm cực trị là
A. (0;6)
B. (6;33)
C. (1;33)
D. (1;6)
