Đường cong ở hình bên là đồ thị của hàm số y = a x + b c x + d với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng?
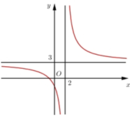
A. y ' < 0 ∀ x ≠ 2
B. y ' < 0 ∀ x ≠ 3
C. y ' > 0 ∀ x ≠ 3
D. y ' > 0 ∀ x ≠ 2
Những câu hỏi liên quan
Đường cong ở hình vẽ bên là đồ thị của hàm số y=f(x).
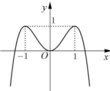
Số nghiệm của phương trình 2f(x)-1=0 là
A. 2.
B. 4.
C. 0.
D. 3.
Cho hàm số
y
f
(
x
)
x
3
-
3
x
2
+
2
có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số
y
x
+
1
? A. B. C. D.
Đọc tiếp
Cho hàm số y = f ( x ) = x 3 - 3 x 2 + 2 có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số y = x + 1 ?
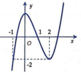
A.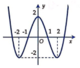 
B.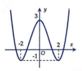 
C. 
D.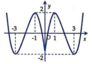 
Đáp án C.
Tịnh tiến đồ thị hàm số y = f x sang trái 1 đơn vị.
Giữ nguyên phần đồ thị hàm số nằm bên phải trục tung. Xóa phần đồ thị hàm số nằm bên trái trục tung.
Lấy đối xứng phần đồ thị hàm số nằm bên phải trục tung qua trục tung.
Từ đây ta có đồ thị hàm số y = f x + 1 .
Đúng 0
Bình luận (0)
Đường cong ở hình vẽ bên dưới là đồ thị của hàm số
y
a
x
4
+
b
x
2
+
c
với a, b, c là các số thực. A. Phương trình y 0 vô nghiệm trên tập số thực B. Phương trình y 0 có ba nghiệm thực phân biệt C.Phương trình y 0 có hai nghiệm thực phân biệt D. Phương trình y 0 có đúng một nghiệm thực
Đọc tiếp
Đường cong ở hình vẽ bên dưới là đồ thị của hàm số y = a x 4 + b x 2 + c với a, b, c là các số thực.
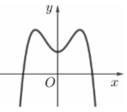
A. Phương trình y ' = 0 vô nghiệm trên tập số thực
B. Phương trình y ' = 0 có ba nghiệm thực phân biệt
C.Phương trình y ' = 0 có hai nghiệm thực phân biệt
D. Phương trình y ' = 0 có đúng một nghiệm thực
Đáp án B
Phương pháp:
Quan sát đồ thị, đếm số cực trị của đồ thị hàm số và suy ra số nghiệm của phương trình y ' = 0 .
Cách giải:
Đồ thị hàm số có 3 điểm cực trị hay hàm số có 3 điểm cực trị. Do đó phương trình y ' = 0 có ba nghiệm thực phân biệt.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục, có đạo hàm f(x) với mọi x và đồ thị của hàm số yf(x) là đường cong cho ở hình vẽ bên. Mệnh đề nào dưới đây đúng A.
H
à
m
s
ố
f
(
x
)
đ
ồ
n
g
b
i
ế
n
t
r
ê
n
k
h
o
ả
n
g
...
Đọc tiếp
Cho hàm số y=f(x) liên tục, có đạo hàm f'(x) với mọi x và đồ thị của hàm số y=f'(x) là đường cong cho ở hình vẽ bên. Mệnh đề nào dưới đây đúng
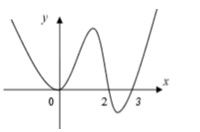
A. H à m s ố f ( x ) đ ồ n g b i ế n t r ê n k h o ả n g ( - ∞ ; 2 ) v à ( 3 ; + ∞ )
b. H à m s ố f ( x ) n g h ị c h b i ế n t r ê n k h o ả n g ( - ∞ ; 2 ) v à ( 3 ; + ∞ )
C. H à m s ố f ( x ) đ ồ n g b i ế n t r ê n k h o ả n g ( 2 ; 3 )
D. H à m s ố f ( x ) n g h ị c h b i ế n t r ê n k h o ả n g ( 0 ; 2 )
Cho hàm số y=f(x) liên tục trên R và có đồ thị là đường cong như hình vẽ bên. Tìm điểm cực tiểu của đồ thị hàm số y=f(x).
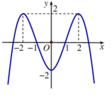
A. y=-2
B. x=0
C. M(0;-2)
D. N(2;2)
Đáp án C
Nhìn vào đồ thị thì điểm cực tiểu là điểm M(0;-2)
Đúng 0
Bình luận (0)
Đường cong ở hình vẽ bên dưới là đồ thị của hàm số y ax 4 + bx 2 + c với a, b, c là các số thực A. Phương trình y 0 vô nghiệm trên tập số thực B. Phương trình y 0 có ba nghiệm thực phân biệt C.Phương trình y 0 có hai nghiệm thực phân biệt D. Phương trình y 0 có đúng một nghiệm thực
Đọc tiếp
Đường cong ở hình vẽ bên dưới là đồ thị của hàm số y = ax 4 + bx 2 + c với a, b, c là các số thực
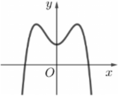
A. Phương trình y ' = 0 vô nghiệm trên tập số thực
B. Phương trình y ' = 0 có ba nghiệm thực phân biệt
C.Phương trình y ' = 0 có hai nghiệm thực phân biệt
D. Phương trình y ' = 0 có đúng một nghiệm thực
Chọn B
Đồ thị hàm số có 3 điểm cực trị hay hàm số có 3 điểm cực trị.
Do đó phương trình y ' = 0 có ba nghiệm thực phân biệt
Đúng 0
Bình luận (0)
Đường cong ở hình bên là đồ thị của hàm số nào dưới A.
y
x
4
+
2
x
2
B.
y
x
4
-
2
x
2
C.
y
-
x
4
-
2
x
2
D.
y
-...
Đọc tiếp
Đường cong ở hình bên là đồ thị của hàm số nào dưới
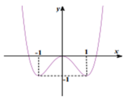
A. y = x 4 + 2 x 2
B. y = x 4 - 2 x 2
C. y = - x 4 - 2 x 2
D. y = - x 4 + 2 x 2
Chọn đáp án B
Đồ thị hướng lên , 3 điểm cực trị
Đúng 0
Bình luận (0)
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? A.
y
−
2
x
3
−
6
x
2
−
6
x
+
1
B.
y
2
x
3
−
6
x
2
+
6
x
+
1
C.
y...
Đọc tiếp
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
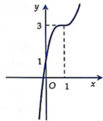
A. y = − 2 x 3 − 6 x 2 − 6 x + 1
B. y = 2 x 3 − 6 x 2 + 6 x + 1
C. y = 2 x 3 − 6 x 2 − 6 x + 1
D. y = 2 x 3 − x 2 + 6 x + 1
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? A.
y
−
2
x
3
−
6
x
2
−
6
x
+
1
B.
y
2
x
3
−
6
x
2
+
6
x
+
1
C.
y...
Đọc tiếp
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
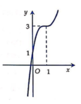
A. y = − 2 x 3 − 6 x 2 − 6 x + 1
B. y = 2 x 3 − 6 x 2 + 6 x + 1
C. y = 2 x 3 − 6 x 2 − 6 x + 1
D. y = 2 x 3 − x 2 + 6 x + 1
Đáp án B
Với x = 1 thì y=3 nên ta loại A; C, D chọn B.
Đúng 0
Bình luận (0)
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? A.
y
−
2
x
3
−
6
x
2
−
6
x
+
1
B.
y
2
x
3
−
6
x...
Đọc tiếp
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
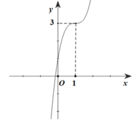
A. y = − 2 x 3 − 6 x 2 − 6 x + 1
B. y = 2 x 3 − 6 x 2 + 6 x + 1
C. y = 2 x 3 − 6 x 2 − 6 x + 1
D. y = 2 x 3 − 6 x 2 + 6 x + 1
Đáp án B
Xét hàm số ax3 + bx2+cx+d=0
Do ĐTHS đông biến có chiều hướng lên nên suy ra a > 0 => Loại A
Theo hình vẽ ta thấy ĐTHS qua các điểm (1,3), (0,1)
Thử 3 đáp án suy ra B
Đúng 0
Bình luận (0)