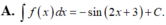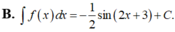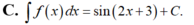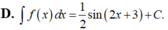Tìm nguyên hàm của hàm số f (x) = cosx.
A. ∫ cos x d x = - 1 2 sin x + C
B. ∫ cos x d x = - sin x + C
C. ∫ cos x d x = sin 2 x + C
D. ∫ cos x d x = sin x + C
Những câu hỏi liên quan
Cho
F
(
x
)
1
4
x
4
+
1
3
x
3
là một nguyên hàm của hàm số f(x). Tìm nguyên hàm của hàm số f’(x)cosx A.
∫
f
x
cos
x
d
x
2
x
+
1...
Đọc tiếp
Cho F ( x ) = 1 4 x 4 + 1 3 x 3 là một nguyên hàm của hàm số f(x). Tìm nguyên hàm của hàm số f’(x)cosx
A. ∫ f ' x cos x d x = 2 x + 1 sin x - 2 cos x + C
B. ∫ f ' x cos x d x = 2 x + 1 sin x + 2 cos x + C
C. ∫ f ' x cos x d x = - 2 x + 1 sin x - 2 cos x + C
D. ∫ f ' x cos x d x = - 2 x + 1 sin x + 2 cos x + C
Tìm nguyên hàm của hàm số
f
(
x
)
(
sin
x
+
c
o
s
x
)
2
A.
∫
f
(
x
)
d
x
x
+
1
2
c
o
s...
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = ( sin x + c o s x ) 2
A. ∫ f ( x ) d x = x + 1 2 c o s 2 x + C
B. ∫ f ( x ) d x = 1 2 c o s 2 x + C
C. ∫ f ( x ) d x = - 1 2 c o s 2 x + C
D. ∫ f ( x ) d x = x - 1 2 c o s 2 x + C
Tìm nguyên hàm F(x) của hàm số f(x)sinx+cosx thỏa mãn
F
π
2
2
A. F (x) -cosx +sinx+1 B. F (x) -cosx+sinx-1 C. F(x) cosx-sinx +3 D. F (x) -cosx+sinx +3
Đọc tiếp
Tìm nguyên hàm F(x) của hàm số f(x)=sinx+cosx thỏa mãn F π 2 = 2
A. F (x)= -cosx +sinx+1
B. F (x)= -cosx+sinx-1
C. F(x)= cosx-sinx +3
D. F (x)= -cosx+sinx +3
Tìm nguyên hàm của hàm số f(x) x cos x A. B. C. D.
Đọc tiếp
Tìm nguyên hàm của hàm số f(x) = x cos x
A. 
B. 
C. 
D. 
Tìm nguyên hàm của hàm số
f
(
x
)
(
sin
x
+
cos
x
)
2
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = ( sin x + cos x ) 2
Tìm nguyên hàm của hàm số f(x) = cos 5x
Cho hàm số F(x) là một nguyên hàm của hàm số
f
(
x
)
sin
3
x
.
cos
x
. Tính
I
F
π
2
-
F
(
0
)
Đọc tiếp
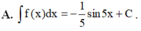
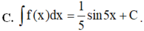
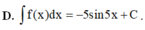
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = sin 3 x . cos x . Tính I = F π 2 - F ( 0 )
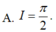
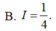
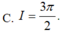
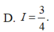
Tìm nguyên hàm F(x) của hàm số \(f\left(x\right)=\cos x+\sin x\) sao cho nguyên hàm đó thỏa mãn điều kiện F(0)=1
Một trong các nguyên hàm của hàm số \(f\left(x\right)=\cos x+\sin x\) là hàm số \(\sin x-\cos x\) . Từ định lí nếu hàm số f(x) có nguyên hàm F(x) trên khoảng (a,b) thì trên khoảng đó nó có vô số nguyên hàm và hai nguyên hàm bất kì của cùng một hàm cho trên khoảng (a,b) là sai khác nhau một hằng số cộng. suy ra mọi nguyên hàm số đã cho đều có dạng \(F\left(x\right)=\sin x-\cos x+C\), trong đó C là hằng số nào đó.
Để xác định hằng số C ta sử dụng điều kiện F(0)=1
Từ điều kiện này và biểu thức F(x) ta có :
\(\sin0-\cos0+C=1\Rightarrow C=1+\cos0=2\)
Do đó hàm số \(F\left(x\right)=\sin x-\cos x+2\) là nguyên hàm cần tìm
Đúng 0
Bình luận (0)
Tìm họ nguyên hàm của hàm số: f(x)=cos(2x+3)
