Từ khai triển biểu thức 2 x − 1 2018 thành đa thức, tính tổng các hệ số bậc chẵn của đa thức nhận được
A. 3 2018 + 1 2
B. 3 2018 - 1 2
C. 3 2018 + 1
D. 3 2018 - 1
Từ khai triển biểu thức 2 x − 1 2018 thành đa thức, tính tổng các hệ số bậc chẵn của đa thức nhận được
A. 3 2018 + 1 2
B. 3 2018 − 1 2
C. 3 2018 + 1
D. 3 2018 − 1
Đáp án A
Tổng các hệ số bậc chẵn khi khai triển đa thức 2 x − 1 2018 được tính bằng
S = C 2018 0 .2 2018 + C 2018 2 .2 2016 + C 2018 4 .2 2014 + ... + C 2018 2018 .2 0
Ta có x + 1 2018 = ∑ k = 0 2018 C 2018 k x 2018 − k ; − x + 1 2018 = ∑ k = 0 2018 C 2018 k − x 2018 − k
Cộng hai vế đẳng thức trên ta được
x + 1 2018 + − x + 1 2018 = 2 ( C 2018 0 x 2018 + C 2018 2 x 2016 + C 2018 4 x 2014 + ... + C 2018 2018 x 0 )
Với x = 2 ta có 3 2018 + 1 = 2. S ⇒ S = 3 2018 + 1 2
Tính tổng các hệ số khi khai triển đa thức P(x) = (x^3 − 2x^2 + 2)^2018 .
Tổng các hệ số phi khai triển đa thức \(P\left(x\right)\)là \(P\left(1\right)\).
\(P\left(1\right)=\left(1^3-2.1^2+2\right)^{2018}=1^{2018}=1\)
Từ khai triển biểu thức \(\left(3x-4\right)^{17}\) thành đa thức, hãy tính tổng các hệ số của đa thức nhận được ?
Tổng các hệ số của đa thức f(x) = (3x – 4)17 bằng:
f(1) = (3 – 4)17= (– 1)17 = -1
Tìm khai triển biểu thức 3 x - 4 17 thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.
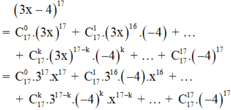
Đặt S là tổng các hệ số của đa thức khai triển.
Ta có:
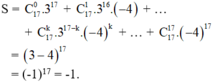
Vậy tổng các hệ số của đa thức khai triển bằng -1.
cho đa thức F(x)= (2017x-2018)2019
khi khai triển ta đc đa thức bậc 2019
Tính tổng các hệ số của các số hạng của đa thức sau khi khai triển
Bài 3: Cho đa thức H(x) = ( 2x – 1)20.
a) Tính tổng hệ số của đa thức H(x) khi khai triển .
b) Tính tổng hệ số bậc chẵn trừ tổng hệ số bậc lẽ của đa thức H(x) khi khai triển .
Tính tổng các hệ số của các hạng tử của đa thức nhận được sau khi đã triển khai và viết đa thức dưới dạng thu gọn
(x4+4x2-5x+1)2017.(2x4-4x2+4x-1)2018
Đặt \(A\left(x\right)=\left(x^4+4x^2-5x+1\right)^{2017}.\left(2x^4-4x^2+4x-1\right)^{2018}\)
Gọi đa thức A(x) sau khi bỏ dấu ngoặc là :
\(A\left(x\right)=a_{32280}x^{32280}+a_{32279}x^{32279}+....+a_1x+a_0\)
Ta thấy tổng giá trị các hệ số của đa thức \(a_{32280}+a_{32279}+...+a_1+a_0\)chính là giá trị của đa thức tại \(x=1\)
Ta có \(A\left(1\right)=\left(1^4+4.1^2-5.1+1\right)^{2017}.\left(2.1^4-4.1^2+4.1-1\right)^{2018}=0\)
Vì \(A\left(1\right)=0\)nên \(a_{32280}+a_{32279}+...+a_1+a_0=0\)
Vậy tổng các hệ số của đa thức sau khi bỏ dấu ngoặc bằng 0
Có bao nhiêu số hạng trong khai triển nhị thức ( 2 x - 3 ) 2018 thành đa thức.
A. 2018
B. 2019
C. 2020
D. 2017
Chọn B
![]()
![]()
![]()
Vậy khai triển trên có 2019 số hạng.
Tìm số hạng chứa x 3 y 3 trong khai triển biểu thức x + 2 y 6 thành đa thức.
A. 160 x 3 y 3
B. 120 x 3 y 3
C. 20 x 3 y 3
D. 8 x 3 y 3
Đáp án A
Ta có: x + 2 y 6 = ∑ k = 0 6 C 6 k x 6 − k 2 y k = ∑ k = 0 6 C 6 k 2 k x 6 − k y k .
Số hạng chứa x 3 y 3 ⇒ 6 − k = 3 k = 3 ⇒ k = 3 ⇒ a 3 = C 6 3 2 3 x 3 y 3 = 160 x 3 y 3 .