Có bao nhiêu giá trị nguyên dương của m không lớn hơn 2018 để hàm số y = x 3 - 6 x 2 + ( m - 1 ) x + 2018 đồng biến trên khoảng (1;+∞)?
A. 2005
B. 2017
C. 2018
D. 2006
Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2018 để hàm số y = 2 x 3 + 3 ( m - 1 ) x 2 + 6 ( m - 2 ) x + 3 nghịch biến trên khoảng có độ dài lớn hơn 3.
A. 2009
B. 2010
C. 2011
D. 2012
Có bao nhiêu giá trị nguyên dương của m, không lớn hơn 2018, sao cho giá trị nhỏ nhất của hàm số y = m x 3 3 − x 2 − m − 2019 x + 1 trên đoạn [6;9] luôn lớn hơn 69069 ?
A. 1069.
B. 1696.
C. 1801.
D. 1155.
Có bao nhiêu giá trị nguyên của m lớn hơn -2018 để hàm số y = − x 3 − 3 x 2 + 4 m x − 2018 nghịch biến trên ( − ∞ ; 0 ) ?
A. 2017
B. 2018
C. 2019
D. Vô số
Có bao nhiêu giá trị nguyên của m lớn hơn -2018 để hàm số y = − x 3 − 3 x 2 + 4 m x − 2018 nghịch biến trên ( − ∞ ; 0 ) ?
A. 2017
B. 2018.
C. 2019
D. Vô số
Đáp án A.
Ta có y ' = − 3 x 2 − 6 x + 4 m =>Hàm số nghịch biến trên − ∞ ; 0
⇔ y ' ≤ 0 ∀ x ∈ − ∞ ; 0 ⇔ 4 m ≤ 3 x 2 + 6 x ∀ x ∈ − ∞ ; 0
Bảng biến thiên:
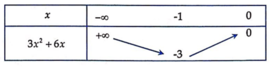
⇒ 3 x 2 + 6 x ≥ − 3 ∀ x ∈ − ∞ ; 0 ⇒ 4 m ≤ 3 x 2 + 6 x ∀ x ∈ − ∞ ; 0
⇔ 4 m ≤ − 3 ⇔ m ≤ − 3 4 ⇒ m ∈ − 2018 ; − 3 4 m ∈ ℤ
Cho hàm số y = 1 3 x 3 − 2 m + 1 x 2 − m x + 2018 . Hỏi có bao nhiêu giá trị nguyên dương của hàm số m để hàm số có hai điểm cực trị x 1 , x 2 ( x 1 < x 2 ) thỏa mãn x 1 > x 2 .
A. 2
B. 1
C. 0
D. vô số
Cho hàm số y = 1 3 x 3 − 2 m + 1 x 2 − m x + 2018 . Hỏi có bao nhiêu giá trị nguyên dương của hàm số m để hàm số có hai điểm cực trị x 1 , x 2 ( x 1 < x 2 ) thỏa mãn x 1 > x 2 .
A. 2
B. 1
C. 0
D. vô số
Đáp án C.
y ' = x 2 − 2 2 m + 1 x − m ; y ' = 0 ⇔ x 2 − 2 2 m + 1 x − m = 0 (*).
Δ ' = 2 m + 1 2 + m = 4 m 2 + 5 m + 1
Để hàm số có hai điểm cực trị thì y ' = 0 có hai nghiệm phân biệt.
Khi đó hai điểm cực trị x 1 , x 2 là hai nghiệm của phương trình (*).
Xét các trường hợp sau:
+ Phương trình (*) có nghiệm bằng 0 ⇒ m = 0 .
Với m = 0 , (*) trở thành x 2 − 2 x = 0 ⇔ x 1 = 0 x 2 = 2 , không thỏa mãn x 1 < x 2 mà x 1 > x 2 .
+ Phương trình (*) có nghiệm 0 < x 1 < x 2 . Khi đó x 1 < x 2 nên trường hợp này không thỏa mãn.
+ Phương trình (*) có nghiệm x 1 < 0 < x 2 .
Khi đó ta có
x 1 > x 2 ⇔ − x 1 > x 2 ⇔ x 1 + x 2 < 0
Vậy điều kiện cho trường hợp này là
P < 0 S < 0 ⇔ − m < 0 2 2 m + 1 < 0 ⇔ m > 0 m < − 1 2
hệ này vô nghiệm.
+ Phương trình (*) có nghiệm x 1 < x 2 < 0 . Khi đó ta có ngay x 1 > x 2 .
Vậy điều kiện cho trường hợp này là
Δ ' > 0 P > 0 S < 0 ⇔ 4 m 2 + 5 m + 1 > 0 − m > 0 2 2 m + 1 < 0 ⇔ m ∈ − ∞ ; − 1 ∪ − 1 4 ; + ∞ m < 0 m < − 1 2 ⇔ m ∈ − ∞ ; − 1
Vậy không có giá trị nguyên dương nào của m thỏa mãn yêu cầu bài toán.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018; 2018] để hàm số y = (m – 2)x + 2m đồng biến trên R.
A. 2015
B. 2017
C. Vô số
D. 2016
Hàm số bậc nhất đồng biến suy ra a > 0 hay m > 2
m thuộc đoạn [-2018; 2018] suy ra m thuộc {3; 4; ...; 2018}
Vậy có 2016 giá trị nguyên của m cần tìm.
Chọn D.
Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây: có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 2018 ) + m 2 có 5 điểm cực trị
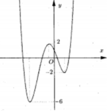
B. 1
C. 2
D. 3
Cho hàm số f ' x = x - 2 2 x 2 - 4 x + 3 với mọi x ∈ ℝ . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f x 2 - 10 x + m + 9 có 5 điểm cực trị?
A. 17.
B. 18.
C. 15.
D. 16.