Giải bất phưong trình x − 2 4 < x + 1 6 và minh họa tập nghiệm trên trục số

Những câu hỏi liên quan
Giải bất phưong trình x − 2 4 < x + 1 6 và minh họa tập nghiệm trên trục số
Giải các phưong trình tích sau : a.x-5=1/3(x+2) b.x/3+x/4=1/5-x/6 c.x/2+x/3=1/4-x/5 d.(x+1)^2-5=x^2+11
Giải và biện luận phưong trình
a . ( x - 1 ) = 2 . ( b - x )
Bài 1: Giải các bất phương trình:
3(1 - x)> \(\dfrac{7-3x^2}{x+1}\)
Bài 2. Giải và biện luận bất phương trình
( m2 - 4 ) x +3 > ( 2m -1) x +m
Giải hệ phưong trình
2(2y^2+1)√x=(5xy+3y^2-2)√y
xy+y^2=2
Câu 2 trong http://i.imgur.com/iS5YuoV.jpg nhé!
giải phương trình và bất phương trình
/x-5/=2x
(x-2)^2+2(x-1)<=x^2+4
\(\left|x-5\right|=2x\)ĐK : x>=0
TH1 : x - 5 = 2x <=> x = -5 ( loại )
TH2 : x - 5 = -2x <=> 3x = 5 <=> x = 5/3 ( tm )
Vậy tập nghiệm pt là S = { 5/3 }
\(\left(x-2\right)^2+2\left(x-1\right)\le x^2+4\)
\(\Leftrightarrow x^2-4x+4+2x-2-x^2-4\le0\)
\(\Leftrightarrow-2x-2\le0\Leftrightarrow x+1\ge0\Leftrightarrow x\ge-1\)
Vậy tập nghiệm bft là S = { x | x > = -1 }
Đúng 1
Bình luận (0)
Ta có: \(\left|x-5\right|=2x\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=2x\left(x\ge5\right)\\x-5=-2x\left(x< 5\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2x=5\\x+2x=5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-x=5\\3x=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\left(loại\right)\\x=\dfrac{5}{3}\left(nhận\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm m để phưong trình sau có nghiệm
4
−
x
+
4
+
x
3
−
6
16
−
x
2
+
2
m
+
1
0
A.
m
∈...
Đọc tiếp
Tìm m để phưong trình sau có nghiệm 4 − x + 4 + x 3 − 6 16 − x 2 + 2 m + 1 = 0
A. m ∈ ℝ
B. m > − 1 − 16 2 2
C. − 41 2 ≤ m ≤ − 1 − 16 2 2
D. m < − 41 2
Đáp án C
4 − x + 4 + x 3 − 6 16 − x 2 + 2 m + 1 = 0 (*) ĐK x ∈ − 4 ; 4
Đặt S = 4 − x + 4 + x , S ∈ 2 2 ; 4 P = 4 − x . 4 + x = 16 − x 2 , P ∈ 0 ; 4
Khi đó phương trình đã cho trở thành
S 3 − 6 P + 2 m + 1 = 0 S 2 = 2 P + 8 ⇔ P = S 2 − 8 2 S 3 − 6 S 2 − 8 2 + 2 m + 1 = 0 ⇔ P = S 2 − 8 2 ( 1 ) S 3 − 3 S 2 + 24 + 2 m + 1 = 0 ( 2 )
Để phương trình (*) có nghiệm
hệ phương trình trên có nghiệm S ≥ 2 2 , P ≥ 0 và S 2 > 4 P
phương trình (2) có nghiệm S ∈ 2 2 ; 4
f ( S ) = S 3 − 3 S 2 + 25, S ∈ 2 2 ; 4 f ' ( S ) = 3 S 2 − 6 S f ' ( S ) = 0 ⇔ S = 0 ( L ) S = 2 ( L )
Bảng biến thiên
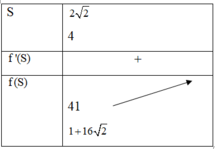
Đúng 0
Bình luận (0)
Giải phương trình và bất phương trình: 9/x^2-4 = x-1/x+2 +3/x -2
\(\frac{9}{x^2-4}=\frac{x-1}{x+2}+\frac{3}{x-2}\)
\(ĐKXĐ:x\ne\pm2\)
\(pt\Leftrightarrow\frac{9}{x^2-4}=\frac{x^2-3x+2}{x^2-4}+\frac{3x+6}{x^2-4}\)
\(\Leftrightarrow\frac{9}{x^2-4}=\frac{x^2+8}{x^2-4}\)
\(\Leftrightarrow x^2+8=9\Leftrightarrow x=\pm1\left(tm\right)\)
Vậy pt có 2 nghiệm là 1 và -1
Đúng 0
Bình luận (0)
Điều kện : \(x+2\ne0\) và \(x-2\ne0\Leftrightarrow x=\pm2\)
( Khi đó \(x^2-4=\left(x+2\right)\left(x-2\right)\ne0\) )
\(\frac{9}{x^2-4}=\frac{x-1}{x+2}+\frac{3}{x-2}\)
\(\Leftrightarrow\frac{9}{\left(x-2\right)\left(x+2\right)}=\frac{\left(x-1\right)\left(x-2\right)+3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow x^2-3x+2+3x+6=9\Leftrightarrow x^2=1\Leftrightarrow x=\pm1\)
Vậy tập nghiệm của PT là: \(S=\left\{-1;1\right\}\)
Chúc bạn học tốt !!!
Đúng 2
Bình luận (0)
giải bất phương trình: |x-4|<x^2+x+1















