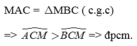cho đoạn thẳng AB có M là trung điểm . Qua M kẻ đường thẳng d vuông góc với AB . Lấy C thuộc d . Chứng minh CM là tia phân giác của ACB

Những câu hỏi liên quan
Cho đoạn thẳng AB có M là trung điểm. Qua M kẻ đường thẳng d vuông góc với AB. Lấy C ∈ d ( C ≠ M ) . Chứng minh CM là tia phân giác của góc ACB
Cho đoạn thẳng AB có M là M là trung điểm. Qua M kẻ đường thẳng d vuông góc với AB. Lấy cd (c \(\ne\)M). Chứng minh CM là tia phân giác của góc ACB
Xem chi tiết
Xét ΔCMA vuông tại M và ΔCMB vuông tại M có
CM chung
MA=MB
Do đó: ΔCMA=ΔCMB
=>\(\widehat{ACM}=\widehat{BCM}\)
=>CM là phân giác của góc ACB
Đúng 0
Bình luận (0)
Qua trung điểm M của đoạn thẳng AB, vẽ đường thẳng vuông góc với AB, trên đường thắng đó lấy C. (C không thuộc M) . Chứng minh rằng tam giác ABC cân và CM là tia phân giác của góc ACB
Ta có: M1^ + M2^ = 180o hay M1^ + 90o = 180o
=> M1^ = 180o - 90o = 90o
=> M1^ = M2^ = 90o
Xét ΔKAM và ΔKBM có:
KM Cạnh chung
M1^ = M2^ = 90o (cmt)
AM = BM (gt)
=> ΔKAM = ΔKBM (c.g.c)
=> K1^ = K2^ (2 góc tương ứng)
=> KM là tia phân giác của AKB^ (ĐPCM)
Bài làm
Xét tam giác CAM và tam giác ABM có:
AM = MB ( Do M là trung điểm AB )
/ CMA = / CMB ( cùng = 90o )
CM chung
=> Tam giác CAM = tam giác ABM ( c.g.c )
=> CA = CB ( hai cạnh tương ứng )
=> Tam giác CAB cân tại C
Vì tam giác CAM = tam giác ABM ( cmt )
=> / ACM = / BCM ( hai góc tương ứng )
=> CM là tia phân giác của góc ACB ( đpcm )
Qua trung điểm M của đoạn thẳng AB kẻ đường thẳng d vuông góc với AB. Trên đường thẳng d lấy 2 điểm H và K sao cho M là trung điểm của HK. Chứng minh AB là tia phân giác của góc HAK và HK là tia phân giác của góc AHB
Cho đoạn thẳng AB. Gọi I là trung điểm của đoạn thẳng AB. Qua I, kẻ đường thẳng d vuông góc với AB. Lấy C,D là hai điểm bất kì trên đường thẳng d. Chứng minh rằng:
A: tam giác ACI = tam giác BCI; tam giác ADI = tam giác BDI
B: tam giác ACB = tam giác BCD
C: CD là tia phân giác của góc ACB
Qua trung điểm M của đoạn thẳng AB kẻ đường thẳng d vuông góc với AB. Trên đường thẳng d lấy hai điểm H và K sao cho M là trung điểm của HK. Chứng minh AB là tia phân giác của góc HAK và HK là tia phân giác của góc AHB
Cho tam giác vuông tại A (ABAC) . Kẻ AH vuông góc ( H thuộc BC).Lấy điểm D thuộc tia đối của tia HA sao cho HDHA a) Chứng minh rằng tam giác CAH tam giác CDH và tia CB là tia phân giác của ACD b) Qua D kẻ một đường thẳng song song với AC cắt BC ở M. Chứng minh rằng tam giác CAH tam giác MDH và AD là đường trung trực của đoạn CM c) Kẻ BN vuông góc với đường thẳng AM ( N thuộc tia AM ) . Chứng minh rằng ba điểm B , N , D thẳng hàng.
Đọc tiếp
Cho tam giác vuông tại A (AB>AC) . Kẻ AH vuông góc ( H thuộc BC).Lấy điểm D thuộc tia đối của tia HA sao cho HD=HA a) Chứng minh rằng tam giác CAH= tam giác CDH và tia CB là tia phân giác của ACD b) Qua D kẻ một đường thẳng song song với AC cắt BC ở M. Chứng minh rằng tam giác CAH= tam giác MDH và AD là đường trung trực của đoạn CM c) Kẻ BN vuông góc với đường thẳng AM ( N thuộc tia AM ) . Chứng minh rằng ba điểm B , N , D thẳng hàng.
qua trung điểm M của đoạn thẳng AB kẻ đoạn thẳng d vuông góc với AB.lầy điểm C trên đoạn thẳng d.C/m CM là tia phân giác của góc ACB
bạn tự vẽ hình nhé
Xét tam giác vuông ACM và tam giác vuông BCM có
\(AM=BM\left(Gt\right)\)
CM chung
=> tam giác vuông ACM = tam giác vuông BCM (T/C tam giác vuông )
=> \(\widehat{ACM}=\widehat{BCM}\)(2 góc tương ứng)
=> CM là tia phân giác của \(\widehat{ACB}\)
Đúng 0
Bình luận (0)
Cho đường tròn (O), AB 2R. Trên đoạn thẳng AO lấy điểm H bất kì không trùng với A và O, kẻ đường thẳng d vuông góc với AB tại H, trên d lấy điểm C nằm ngoài đường tròn, từ C kẻ hai tiếp tuyến CM, CN với (O), M và N là các tiếp điểm (M thuộc nửa mp bờ d có chứa điểm A). Gọi P và Q lần lượt là giao điểm của CM, CN với đường thẳng AB.a) Chứng minh HC là tia phân giác của góc MHN.b) Đường thẳng qua O vuôn góc với AB cắt MN tại K và đường thẳng CK cắt đường thẳng AB tại I. Chứng minh I là trung điểm...
Đọc tiếp
Cho đường tròn (O), AB = 2R. Trên đoạn thẳng AO lấy điểm H bất kì không trùng với A và O, kẻ đường thẳng d vuông góc với AB tại H, trên d lấy điểm C nằm ngoài đường tròn, từ C kẻ hai tiếp tuyến CM, CN với (O), M và N là các tiếp điểm (M thuộc nửa mp bờ d có chứa điểm A). Gọi P và Q lần lượt là giao điểm của CM, CN với đường thẳng AB.
a) Chứng minh HC là tia phân giác của góc MHN.
b) Đường thẳng qua O vuôn góc với AB cắt MN tại K và đường thẳng CK cắt đường thẳng AB tại I. Chứng minh I là trung điểm PQ.
Qua trung điểm M của đoạn thẳng AB kẻ đường thẳng d vuông AB.Trên đưòng thẳng d lấy 2 điểm M và K sao cho M là trung điẻm của HK .CM AB là tia phân giác củab góc HAK và HK là tia phân giác của góc AHB