Cho tam giác ABC vuông tại A có AB = 20cm, BC = 25cm. Tính AC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Kẻ đường cao AH cắt BC tại H, biết AB=20cm, AC=25cm, AH=16cm. Tính độ dài BC và Chu vì tam giác ABC
Áp dụng định lý \(Pi-ta -go \) và tam giác vuông \(ABC\) ta có :
\(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(=\sqrt{20^2+25^2}=5\sqrt{41}\) \(\left(cm\right)\)
Chu vi \(\Delta ABC\) là :\(AB+AC+BC=20+25+5\sqrt{41}=45+5\sqrt{41}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB bằng 15cm, AC = 20cm, BC=25cm. Kẻ AH vuoogn góc BC tại H
1) Chứng minh tam giác ABC vuông tại A
2) Gọi S tam giác ABC là diện tích tam giác ABC. Tính diện tích tam giác ABC
3) Tính AH
tính cạnh tam giác
a) cho ∆ABC vuông tại A biết AB = 8cm, BC = 10cm, tính AC
b) cho ∆DEF vuông tại E biết EF=7cm, DF = 25cm, tính ED
c) cho ∆ABC vuông tại C biết CA = 21cm, AB = 29cm, tính BC
d) cho ABC vuông tại A có AB = 30cm. Kẻ AH vuông góc BC ở H. Tính AC và AH biết BH = 18cm, CH = 32cm
e) cho ∆ABC vuông tại A biết AB=15cm, AC=20cm, tính BC
mọi ngouiwf trả lời câu này giúp mik vs
cho tam giác abc vuông tại a có AB=20cm, BC=25cm . a) tính số đo góc B , b) phân giác góc A cắt BC tại E Tính AE
a) Xét ΔABC vuông tại A có
\(\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{20}{25}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq37^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=15cm,AC=20cm,BC=25cm
a)chứng minh tam giác ABC vuông tại a
b)từ B vẽ đường thẳng vuông góc với BC cắt AC kéo dài tại H. tính HC,HA,HB
ai bít vẽ hình vẽ dùm mình với
Bài 1: tính cạnh tam giác
a) cho ∆ABC vuông tại A biết AB = 8cm, BC = 10cm, tính AC
b) cho ∆DEF vuông tại E biết EF=7cm, DF = 25cm, tính ED
c) cho ∆ABC vuông tại C biết CA = 21cm, AB = 29cm, tính BC
d) cho ABC vuông tại A có AB = 30cm. Kẻ AH vuông góc BC ở H. Tính AC và AH biết BH = 18cm, CH = 32cm
e) cho ∆ABC vuông tại A biết AB=15cm, AC=20cm, tính BC
Cho tam giác ABC vuông tại A có AB=15cm, AC=20cm. Độ dài cạnh BC=25cm và số đo góc B lần lượt là
Xét ΔABC vuông tại A có sin B=AC/BC=4/5
nên \(\widehat{B}\simeq53^0\)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC vuông tại A ,có AB=20cm; BC=25cm . Điểm M thuộc cạnh AB
a ) tính AC
b) Qua B vẽ các đường thẳng vuông góc với CM tại H . Cắt AC tại D . Chứng minh tam giác AMC đồng dạng với tam giác HMB
c ) Chứng minh AC . AD= AM . AB
d ) Chứng minh DM vuông góc với BC
شءشيلبتال
ءبسس
سللباتةتثعي
يسل
a, Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A , ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(\Rightarrow AC^2=25^2-20^2\)
\(\Rightarrow AC^2=225\)
\(\Rightarrow AC=15cm\)
Vậy AC = 15cm .
b,Xét tam giác AMC và tam giác HMB có :
góc MAC = góc MHB = 90độ
góc AMC = góc HMB ( đối đỉnh )
Do đó : tam giác AMC đồng dạng với tam giác HMB ( g.g )
c,Xét tam giác ADB và tam giác AMC có :
góc BAD = góc CAM = 90độ
góc ABD = góc ACM ( vì tam giác AMC đồng dạng với tam giác HMB )
Do đó : tam giác ADB đồng dạng với tam giác AMC ( g.g )
\(\Rightarrow\frac{AC}{AB}=\frac{AM}{AD}\)
\(\Rightarrow AC.AD=AM.AB\)
d, Xét tam giác DBC có BA cắt HC tại M :
\(CH\perp BD\)
\(BA\perp DC\)
\(\Rightarrow\)M là trực tâm của tam giác DBC
Vậy DM vuông góc với BC .
Học tốt
Tam giác \(ABC\) có \(AB = 15cm,AC = 20cm,BC = 25cm\). Đường phân giác của góc \(BAC\)cắt \(BC\) tại \(D\). Qua \(D\) vẽ \(DE//AB\left( {E \in AC} \right)\).
a) Tính độ dài các đoạn thẳng \(BD,DC\) và \(DE\).
b) Chứng minh \(ABC\) là tam giác vuông. Tính diện tích tam giác \(ABC\).
c) Tính diện tích tam giác \(ADB,ADE\) và \(DCE\).
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
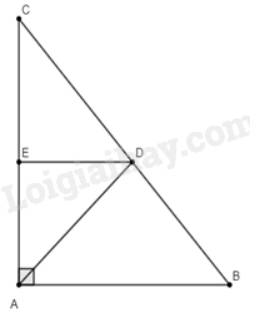
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
Đúng 0
Bình luận (0)
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=25/7
=>DB=75/7cm; DC=100/7cm
Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/15=100/7:25=4/7
=>DE=60/7cm
b: Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
=>S ABC=1/2*15*20=10*15=150cm2
c: DB/DC=3/7
=>S ABD/S ACB=3/7
=>S ABD=150*3/7=450/7cm2
Đúng 0
Bình luận (0)
















