Cho ABC có đường trung tuyến AM và G là trọng tâm của ABC.
Gọi K, N, H lần luợt là các điểm đối xứng của G qua A, B, C. Gọi T là giao
điểm của tia KG với NH.
a) Chứng minh rằng M là trung điểm của GT.
b) Chứng minh rằng G là trọng tâm của KNH.

Những câu hỏi liên quan
cho tam giác ABC có đường trung tuyến AM và G là trọng tâm của tam giác ABC. Gọi K,N,H là các điểm đối xứng của G qua A,B,C. Gọi T là giao điểm của tia KG với NH.
a/ Chứng minh M là trung điểm GT
b/ Chứng minh G là trọng tâm của tam giác KNH
Cho tam giác ABC, đường trung tuyến AM và trọng tâm G. Gọi I là điểm đối xứng với A qua G. Chứng minh rằng I là điểm đối xứng với G qua M.
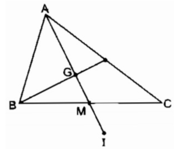
I đối xứng với A qua tâm G
ta có: GA = GI, GM ∈ GA ( tính chất đường trung tuyến của tam giác)
Suy ra: GM ∈ GI
Mà: GM + MI = GI và GM = AG/2 (tính chất đường trung tuyến) =>GM = GI/2
Suy ra: GM = MI nên điểm M là trung điểm của GI
Vậy I đối xứng với G qua M.
Đúng 0
Bình luận (0)
Cho tam giác ABC điểm D đối xứng vs A qua B, E đối xứng B qua C, F đối xứng C qua A Gọi G là giao điểm của đường trung tuyến AM Trong tam giác ABC với trung tuyến DN của tam giác DEF Gọi I, K lần lượt là trung điểm của GA và GD
1) CM tứ giác MNIK là hình bình hành
2) Chứng minh tam giác ABC và tam giác DEF có cùng trọng tâm
LƯU Ý
Các bạn học sinh KHÔNG ĐƯỢC đăng các câu hỏi không liên quan đến Toán, hoặc các bài toán linh tinh gây nhiễu diễn đàn. Online Math có thể áp dụng các biện pháp như trừ điểm, thậm chí khóa vĩnh viễn tài khoản của bạn nếu vi phạm nội quy nhiều lần.
Chuyên mục Giúp tôi giải toán dành cho những bạn gặp bài toán khó hoặc có bài toán hay muốn chia sẻ. Bởi vậy các bạn học sinh chú ý không nên gửi bài linh tinh, không được có các hành vi nhằm gian lận điểm hỏi đáp như tạo câu hỏi và tự trả lời rồi chọn đúng.
Mỗi thành viên được gửi tối đa 5 câu hỏi trong 1 ngày
Các câu hỏi không liên quan đến toán lớp 1 - 9 các bạn có thể gửi lên trang web h.vn để được giải đáp tốt hơn.
Đúng 0
Bình luận (0)
Nối A vs N
a)xét tg CEF có: N là t/đ của EF(gt) và A là t/đ của FC (vì C đx vs F qua A) => AN là đg trung bình của tg CEF
=> AN//CE và AN =1/2. CE
=> AN=1/2.BC(vì BC = CE) => AN =BM(vì BM = 1/2. BC)
xét tg ANMB có: AN=MB (cmt) và AN//MB ( vì AN// CE ; B,M,C,E thẳng hàng) => tg ANMB là hbh=> MN//AB và AB=MN (1) ;
xét tg AGD có: I là t/đ của AG (gt) và K là t/đ của DG(gt) => IK là đg trung bình của tg AGD => IK=1/2.AD và IK //AD
Mà B là t/đ của AD (vì A đx vs D qua B) => AB=BD=1/2.AD=> IK=AB ( =1/2.AD) (2)
Từ (1),(2)=> IK=MN
Ta có: MN// AB(cmt) ; B thuộc AD => MN//AD
Xét tg MNIK có: IK=MN (cmt) và IK//MN (cùng // AD)
=> tg MNIK là hbh (đpcm)
b) Do tg MNIK là hbh ( câu a) mà G là gđ của IM và KN nên G là t/đ của IM là KN
=> IG=MG và KG=NG
Mặt khác: I là t/đ của AG(gt)=> IG=AI=> AI=IG=GM
K là t/đ của DG(gt) => Dk=KG => DK=KG=GN
xét tg ABC có: AM là đg trung tuyến (gt) và AI=IG=GM (cmt) => G là trọng tâm của tg ABC (*)
xét tg DEF có: DN là đg trung tuyến (gt) và DK=KG=GN(cmt) => G là trọng tâm của tg DEF (**)
Từ (*),(**) => G vừa là trọng tam của tg ABC vừa là trọng tâm của tg DEF
=> Tg ABC và tg DEF có cùng trọng tâm là G (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC, đường trung tuyến AM và trọng tâm G. Gọi I là giao điểm đối xứng với A qua G
Chứng minh rằng I là điểm đối xứng với G qua M ?
Vì G là trọng tâm \(\Delta ABC\) (gt)
\(\Rightarrow MG=\dfrac{1}{2}GA=\dfrac{1}{2}GI\) (t/c trọng tâm)
\(\Rightarrow\) MG = MI
\(\Rightarrow\) M là trung điểm của GI (ĐN trung điểm)
\(\Rightarrow\) I đối xứng với G qua M (ĐN đối xứng tâm)
Đúng 0
Bình luận (0)
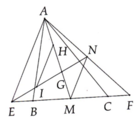
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE CF.a) Chứng minh G là trọng tâm tam giác AEF.b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH MN.
Đọc tiếp
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF.
a) Chứng minh G là trọng tâm tam giác AEF.
b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.
c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH = MN.
Cho tam giác ABC . Gọi A' là điểm đối xứng với A qua C, B' là điểm đối xứng với B qua A , C' đối xứng C qua B . Gọi Bm là đường trung tuyến của tam giác ABC , B'M' là đường trung tuyến của tam giác A'B'C'.
a ) Chứng minh rằng ABM'M là hình bình hành
b) Gọi G là giao điểm của BM và B'M' . Chứng inh rằng G là Trọng tam của hai tam giác ABC và A'B'C'.
Cho tam giác ABC . Gọi A' là điểm đối xứng với A qua C, B' là điểm đối xứng với B qua A , C' đối xứng C qua B . Gọi Bm là đường trung tuyến của tam giác ABC , B'M' là đường trung tuyến của tam giác A'B'C'.
a ) Chứng minh rằng ABM'M là hình bình hành
b) Gọi G là giao điểm của BM và B'M' . Chứng inh rằng G là Trọng tam của hai tam giác ABC và A'B'C'.
Cho tam giác ABC, vẽ điểm A' đối xứng với A qua C, điểm B' đối xứng với B qua A, vẽ điểm C' đối xứng với C qua B. D và D' lần lượt là trung điểm của AC và A'C'. Chứng minh rằng:
a) ABD'D là hình bình hành
b) Gọi O là giao điểm của các đường trung tuyến BD và B'D'. chứng minh O là trọng tâm của tam giác ABC và A'B'C'
cho tam giác ABC vuông tại A , đường trung tuyến AM. Gọi D là trung điểm của AB và G là điểm đối xứng vs điểm M qua D
a, Chứng minh rằng tứ giác AGBM là hbh
b, chứng minh rằng AB _I_ GM
c gọi Q là trung điểm của AM .Chứng minh rằng 3 điểm G;Q;C thẳng hàng
mong mọi người giúp mình vs ạ