Cho hình vuông ABCD tâm O.
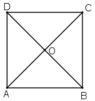
a. Tìm ảnh của điểm C qua phép quay tâm A góc 90 o .
b. Tìm ảnh của đường thẳng BC qua phép quay tâm O góc 90 o
a. Gọi C’ là điểm đối xứng với điểm C qua điểm D.
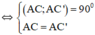⇔ C’ là điểm đối xứng với C qua D.
b) Ta có:
Đúng 0
Bình luận (0)
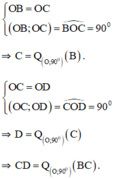
Cho điểm A (-2;3) và đường thẳng (d) 2x-y+3=0 a) tìm ảnh của A qua phép quay tâm O góc quay π/2 b) viết phương trình đường thẳng (d') là ảnh của (d) qua phép quay tâm O góc quay -90°
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có O là giao điểm của hai đường thẳng AC’ và A’C. Xác định ảnh của tứ diện
A
B
’
C
’
D
’
qua phép đối xứng tâm O. A. Tứ diện ABC’D. B. Tứ diện A’BCD. C. Tứ diện AB’CD D. Tứ diện ABCD’
Đọc tiếp
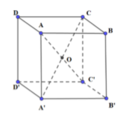
Cho hình lập phương A B C D . A ' B ' C ' D ' có O là giao điểm của hai đường thẳng AC’ và A’C. Xác định ảnh của tứ diện A B ’ C ’ D ’ qua phép đối xứng tâm O.
A. Tứ diện ABC’D.
B. Tứ diện A’BCD.
C. Tứ diện AB’CD
D. Tứ diện ABCD’
Phương pháp:
Phép đối xứng tâm O biến M thành M’=>O là trung điểm của MM’.
Cách giải:
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho các điểm A(3; 3), B(0; 5), C(1; 1) và đường thẳng d có phương trình 5x − 3y + 15 = 0. Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình của đường thẳng d theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90 ο
Cho hình vuông ABCD tâm O. Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90o và phép tịnh tiến theo vectơ biến đoạn thẳng AB thành đoạn thẳng nào trong các đoạn thẳng sau?
A. AB
B. CB
C. DA
D. BC
Trong mặt phẳng Oxy, cho đường thẳng d:5x-2y+3=0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép quay tâm O, góc quay -180 độ
Lấy A(3;9) thuộc (d)
Theo đề, ta có:
\(\left\{{}\begin{matrix}x_{A'}+3=0\\y_{A'}+9=0\end{matrix}\right.\Leftrightarrow A'\left(-3;-9\right)\)
Vì (d1)//(d) nên (d1): 5x-2y+c=0
Thay x=-3 và y=-9 vào (d1), tađược:
c+5*(-3)-2*(-9)=0
=>c-15+18=0
=>c=-3
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho điểm A(2;0) và đường thẳng d có phương trình x + y – 2 = 0 . Tìm ảnh của A và d qua phép quay tâm O góc 90 o .
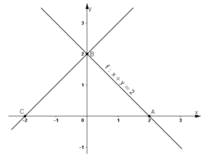
* Ta có A(2; 0) thuộc tia Ox.
Gọi Q(O,90º) (A) = B thì B thuộc tia Oy và OA = OB nên B(0 ; 2).
* Gọi d’ là ảnh của d qua phép quay tâm O, góc quay 90º.
+ A(2 ; 0) ∈ (d)
⇒ B = Q(O,90º) (A) ∈ (d’)
+ B(0 ; 2) ∈ (d).
⇒ C = Q(O,90º) (B) ∈ (d’).
Dễ dàng nhận thấy C(-2; 0) (hình vẽ).
⇒ (d’) chính là đường thẳng BC.
Đường thẳng d’ đi qua B(0 ; 2) và C(-2; 0) nên có phương trình đoạn chắn là:
Đúng 0
Bình luận (0)
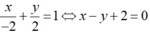
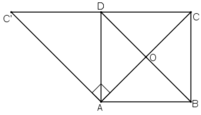
Cho hình chóp S.ABCD có cạnh SA vuông góc với đáy . Đáy là hình vuông tâm O a) Xác định góc giữa đường thăng SB và mặt đáy b) Xác định góc giữa đường thẳng SO và mặt (ABCD) c) Xác định góc giữa đường thẳng SC và mặt (SAD) d) Xác định góc giữa đường SB và mặt (SAC)
a: (SB;(ABCD))=(BS;BA)=góc SBA
b: (SO;(ABCD))=(OS;OA)=góc SOA
c: (SC;(SAD))=(SC;SD)
Đúng 0
Bình luận (0)
Cho hcn ABCD, O là Giao điểm của 2 đường chéo. Đường thẳng qua B, D vuông góc với AC cắt AB, CD tại M, N
a) CM BMDN là hình bình hành
b) CM 3 điểm M, O, N thẳng hàng
c) H là giao điểm của DN, AC. I,K là trung điểm của AH, BC. Tính góc DIK.
Xem chi tiết
Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD. Qua O kẻ các đường thẳng lần lượt vuông góc với AB,BC,CD,DA tại E,G,F,H.Chứng minh:
a) Bà điểm E,O,F thẳng hàng và ba điểm G,O,H thẳng hàng
b) Tứ giác EGFH lầ hình vuông