giải pt:
3cos2x+8sin3xcosx+16cosx=4sin4x+22sinx+23
3cos2x+8sin3xcosx+16cosx=4sin4x+22sinx+23
2sin^2.2x-3cos2x+6sin^2-9=0. Giúp e giải pt này vs ạ
Đề là: \(2sin^22x-3cos2x+6sin^2x-9=0\) đúng không nhỉ?
\(\Leftrightarrow2\left(1-cos^22x\right)-3cos2x+3\left(1-cos2x\right)-9=0\)
\(\Leftrightarrow-2cos^22x-6cos2x-4=0\)
\(\Leftrightarrow cos^22x+3cos2x+2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow...\)
Giải phương trình 1 + tan x = 2 2 sin x
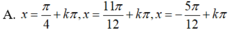
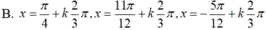
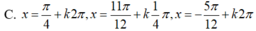
![]()
Giải phương trình sin x + cos x = 2 2 sin x cos x
![]()

![]()
![]()
Giải phương trình lượng giác 4sin4x + 12cos2x – 7 = 0 có nghiệm là
![]()
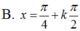
![]()
![]()
Hướng dẫn giải
Chọn B.
Ta có: 4sin4 + 12cos2 x – 7 =0
ó 4sin4x – 12sin2 x + 5= 0
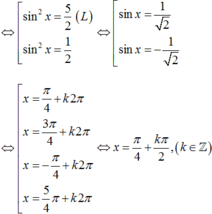
33, giai pt
\(\frac{4sin^22x+6sin^2x-9-3cos2x}{cosx}\)
Giai Pt
\(\left(2sinx-cosx\right)\left(1+cosx\right)=sin^2x\)
\(3sin^2x+7cos2x-3=0\)
\(\dfrac{4sin^2x+6sin^2x-9-3cos2x}{cosx}=0\)
a/ \(\left(2sinx-cosx\right)\left(1+cosx\right)=sin^2x\)
\(\Leftrightarrow\left(2sinx-cosx\right)\left(1+cosx\right)=\dfrac{1-cos2x}{2}\)
\(\Leftrightarrow\left(2sinx-cosx\right)\left(1+cosx\right)=\dfrac{1-2cos^2x+1}{2}=\dfrac{2-2cos^2x}{2}=1-cos^2x\)
\(\Leftrightarrow\left(2sinx-cosx\right)\left(1+cosx\right)=\left(1-cosx\right)\left(1+cosx\right)\Leftrightarrow\left(2sinx-cosx\right)\left(1+cosx\right)-\left(1-cosx\right)\left(1+cosx\right)=0\)\(\Leftrightarrow\left(1+cosx\right)\left(2sinx-cosx-1+cosx\right)=0\Leftrightarrow\left(1+cosx\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}1+cosx=0\\2sinx-1=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=180^o\\x=30^o\end{matrix}\right.\)
a) Đáp án: \(\left[{}\begin{matrix}cosx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)(\(k\in Z\))
Vậy...
b) \(3sin^2x+7cos2x-3=0\)
\(\Leftrightarrow3sin^2x+7\left(1-2sin^2x\right)-3=0\)
\(\Leftrightarrow11.sin^2x=4\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{2\sqrt{11}}{11}\\sinx=\dfrac{-2\sqrt{11}}{11}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=arc.sin\dfrac{2\sqrt{11}}{11}+k2\pi\\x=\pi-arc.sin\dfrac{2\sqrt{11}}{11}+k2\pi\\x=arc.sin\dfrac{-2\sqrt{11}}{11}+k2\pi\\x=\pi-arc.sin\dfrac{-2\sqrt{11}}{11}+k2\pi\end{matrix}\right.\) (\(k\in Z\)) (Dị quá,câu này e ko biết đ/a đúng hay sai đâu)
Vậy...
c)\(\dfrac{4.sin^2x+6.sin^2x-9-3.cos2x}{cosx}=0\) (đk: \(x\ne\dfrac{\pi}{2}+k\pi\),\(k\in Z\))
\(\Rightarrow10sin^2x-9-3\left(1-2.sin^2x\right)=0\)
\(\Leftrightarrow sin^2x=\dfrac{3}{4}\)\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{\sqrt{3}}{2}\\sinx=-\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\\x=\dfrac{-\pi}{3}+k2\pi\\x=\dfrac{4\pi}{3}+k2\pi\end{matrix}\right.\)(\(k\in Z\)) (Thỏa mãn đk)
Vậy...
b/\(3sin^2x+7cos2x-3=0\Leftrightarrow3sin^2x+7\left(2cos^2x-1\right)-3=0\Leftrightarrow3sin^2x+14cos^2x-7-3=0\)\(\Leftrightarrow3sin^2x+3cos^2x+11cos^2x-10=0\Leftrightarrow3+11cos^2x-10=0\Leftrightarrow11cos^2x-7=0\)\(\Leftrightarrow cos^2x=\dfrac{7}{11}\Leftrightarrow cosx=\sqrt{\dfrac{7}{11}}\)\(\Leftrightarrow x=37^o5'\)
Ủa sao kết quả xấu vậy:vvv Chắc sai đâu rồi:vv
Giải phương trình:
a,\(3Cos2x-4Sin2x=1\)
Pt\(\Leftrightarrow3\left(cos^2x-sin^2x\right)-8.sinx.cosx=sin^2x+cos^2x\)
\(\Leftrightarrow2cos^2x-8sinx.cosx-4sin^2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\left(2+\sqrt{6}\right)sinx\\cosx=\left(2-\sqrt{6}\right)sinx\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=\dfrac{1}{2+\sqrt{6}}\\tanx=\dfrac{1}{2-\sqrt{6}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=arc.tan\left(\dfrac{1}{2+\sqrt{6}}\right)+k\pi\\x=arc.tan\left(\dfrac{1}{2-\sqrt{6}}\right)+k\pi\end{matrix}\right.\), k nguyên
Vậy...
Giải pt
2sin^2.2x-3cos2x+6sin^2-9=0