Cho hình chữ nhật ABCD và điểm E trên cạnh AB. Chứng minh rằng: ED+EC\(\le\)AD+AC

Những câu hỏi liên quan
Cho hình chữ nhật ABCD có M thuộc hình chữ nhật và có thể nằm trên cạnh của ABCD .cmr ED+EC\(\le\)AC+AD
Cho hình chữ nhật ABCD . Lấy điểm E trên cạnh AB và biết góc DEC = 90 độ , ED = 3 cm,EC = 4 cm . Tính cạnh AD ?
bài này trong giải toán trên mạng 8 phải ko hả bạn
Đúng 0
Bình luận (0)
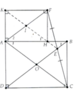
Bài 6. Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo
BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt
vuông góc với AB và AD. Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật.
b) AF song song với BD và KH song song với AC.
999999999999999999999999999999999999
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
H1^ là H mũ 1 à bạn?
Xem thêm câu trả lời
Cho hình chữ nhật ABCD (ABAD). Trên các cạnh AD và BC lấn lượt lấy các điểm E và F sao cho AF CF. a) Chứng minh rằng: AF// CE. b) Gọi O là giao điểm của AC và BD. Chứng minh rằng E đối xửng với F qua O. c) Qua C kẻ đường thẳng vuông góc với tia AF tại H. Chứng minh răng BH vuông góc với DH d) Biết CBH 30°, tỉnh số đo của góc AÔH?
Đọc tiếp
Cho hình chữ nhật ABCD (AB<AD). Trên các cạnh
AD và BC lấn lượt lấy các điểm E và F sao cho AF = CF.
a) Chứng minh rằng: AF// CE.
b) Gọi O là giao điểm của AC và BD. Chứng minh rằng E đối xửng
với F qua O.
c) Qua C kẻ đường thẳng vuông góc với tia AF tại H. Chứng minh
răng BH vuông góc với DH
d) Biết CBH = 30°, tỉnh số đo của góc AÔH?
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE
Đúng 0
Bình luận (0)
Xét hình tứ giác đấy có:
`=>AE//// CF`
`AE=CF`
Có bốn cạnh như trên suy ra là hình bình hành.
`=>` `AF////CE`
Đúng 0
Bình luận (0)
Cho hình vuông ABCD tâm O có độ dài cạnh =6. Gọi E là điểm trên đường thẳng AC thỏa vectơ AC=3 vectơ AE và M là trung điểm AD. Chứng minh đẳng thức vectơ EB+vectơ EC+vectơ ED= vectơ AC
Cho hình chữ nhật ABCD có O là giao điểm của AC và BD. Lấy một điểm E bất kì trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EFEC. Vẽ FH và FK lần lượt vuông góc với AB và AD (H thuộc AB, K thuộc AD).a) Chứng minh: BD2AO.(đã làm)b) Gọi I là giao điểm của KH và AF. Chứng minh I là trung điểm của KH.c) Chứng minh tứ giác AIEO là hình bình hành.d) Chứng minh I, K, E thẳng hàng.
Đọc tiếp
Cho hình chữ nhật ABCD có O là giao điểm của AC và BD. Lấy một điểm E bất kì trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF=EC. Vẽ FH và FK lần lượt vuông góc với AB và AD (H thuộc AB, K thuộc AD).
a) Chứng minh: BD=2AO.(đã làm)
b) Gọi I là giao điểm của KH và AF. Chứng minh I là trung điểm của KH.
c) Chứng minh tứ giác AIEO là hình bình hành.
d) Chứng minh I, K, E thẳng hàng.
a) Để chứng minh BD = 2AO, ta có thể sử dụng định lý Thales và các quy tắc về tỉ lệ đồng dạng. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
b) Để chứng minh I là trung điểm của KH, ta có thể sử dụng các quy tắc về đường thẳng song song và đồng quy. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
c) Để chứng minh tứ giác AIEO là hình bình hành, ta có thể sử dụng các quy tắc về đường chéo và cạnh đối. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
d) Để chứng minh I, K, E thẳng hàng, ta có thể sử dụng các quy tắc về đường thẳng và góc vuông. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD (AB > AD), nối C với một điểm E bất kỳ trên đường chéo BD (\(BE<\frac{1}{2}BD\)), trên tia đối của EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với AB và AD (\(H\in AB,K\in AD\)). Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật
b) AF // BD ; KH // AC
c) Ba điểm E, H, K thẳng hàng
Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:a) Tứ giác AHFK là hình chữ nhật;b) AF song song với BD;c) Ba điểm E, H, K thẳng hàng
Đọc tiếp
Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật;
b) AF song song với BD;
c) Ba điểm E, H, K thẳng hàng
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
Đúng 0
Bình luận (0)
Cho hình 125 trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
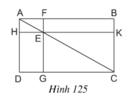
Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK,
ta đi chứng minh SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = AD.DC/2;
SABC = AB.BC/2.
ABCD là hình chữ nhật ⇒ AB = CD, AD = BC
⇒ SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH
⇒ AHEF là hình bình hành
Mà Â = 90º
⇒ AHEF là hình chữ nhật
⇒ SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
EK // GC, EG // KC
⇒ EGCK là hình bình hành
Mà D̂ = 90º
⇒ EGCK là hình chữ nhật
⇒ SEGC = SEKC (3).
Từ (1); (2); (3) suy ra đpcm.
Đúng 0
Bình luận (0)

















