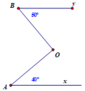
Qua O kẻ d sao cho d / / A x / / B y .

O 1 ^ = 50 ° = y B O ^ ( so le trong); O 2 ^ = O A x ^ = 40 ° ( so le trong) 

⇒ O ^ = 40 ° + 50 ° = 90 °

- hình vẽ này không ss nha bn ơi.

lộn.

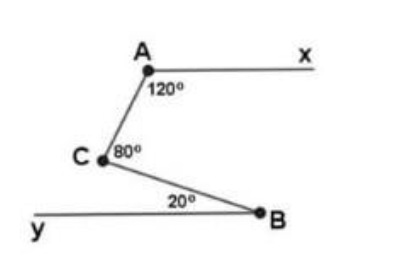
Kẻ Cz song song Ax 

Khi đó \(\widehat{ACz}=180^0-120^0=60^0\)

\(\Rightarrow\widehat{BCz}=80^0-60^0=20^0\)

2 góc, \(\widehat{BCz}\) và \(\widehat{CBy}\) bằng nhau ở vị trí 2 góc so le trong nên Cz song song By. 

\(\Rightarrow Ax//By\) 

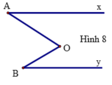
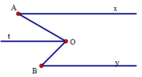Qua điểm O kẻ tia Ot // Ox. Khi đó, A ^ = A O x ^  (2 góc so le trong).

Do O t ∥ O x O y ∥ O x nên   O t ∥ O y ,   B ^ = B O t ^  (2 góc so le trong)

Từ đó, ta có A O B ^ = A O t ^ + t O B ^ = A ^ + B ^ .

Vậy  A ^ + B ^ = A O B ^  (đpcm)

a) Vẽ tia By' là tia đối của tia By

Ta có:

∠ABy' + ∠ABy = 180⁰ (kề bù)

⇒ ∠ABy' = 180⁰ - ∠ABy

= 180⁰ - 135⁰

= 45⁰

⇒ ∠ABy' = ∠BAx = 45⁰

Mà ∠ABy' và ∠BAx là hai góc so le trong

⇒ By // Ax

b) Ta có:

∠CBy' = ∠ABC - ∠ABy'

= 75⁰ - 45⁰

= 30⁰

⇒ ∠CBy' = ∠BCz = 30⁰

Mà ∠CBy' và ∠BCz là hai góc so le trong

⇒ By // Cz

2 góc bù nhau mà ở vị trí trong cùng phía

--> Ax // By

ta có :

A,B,C tỉ lệ với a,b,c

\(\Rightarrow\frac{A}{a}=\frac{B}{b}=\frac{C}{c}\)

đặt \(\frac{A}{a}=\frac{B}{b}=\frac{C}{c}=k\)

\(\Rightarrow\)A = ak ; B = bk ; C = ck

\(\Rightarrow Q=\frac{akx+bky+ck}{ax+by+c}=\frac{k.\left(ax+by+c\right)}{ax+by+c}=k\)

Vậy giá trị của Q không phụ thuộc vào x và y

tự kẻ hình :

xét tam giác AOK và tam giác BOD có : 

AO = OB do O là trung điểm của AB (gt)

góc AOK = góc BOD (đối đỉnh)

góc KAO = góc OBD = 90 do...

=>  tam giác AOK = tam giác BOD (cgv - gnk)

Nếu cái j?