Cho tam giác ABC vuông ở A. Các tia phân giác góc B; C giao nhau tại I. Biết hình chiếu của IB, IC đến BC là 3cm; 5cm. Tính diện tích tam giác ABC

Những câu hỏi liên quan
1. Cho tam giác ABC, góc A 120 độ, AA, BB, CC theo thứ tự là tia phân giác của các góc A, B, C. CMR AB vuông góc với AC.2. Cho tam giác ABC cân ở A. Kẻ tia phân giác BD của góc B và tia phân giác DM của góc BDC, đường phân giác của góc ADB cắt đường thẳng BC tại N. CMR BD 1/2 MN.3. Từ đỉnh A của tam giác ABC, kẻ các đường vuông góc xuống các tia phân giác trong và ngoài của các góc tại đỉnh B và C. CMR chân các đường vuông góc đó thẳng hàng.
Đọc tiếp
1. Cho tam giác ABC, góc A = 120 độ, AA', BB', CC' theo thứ tự là tia phân giác của các góc A, B, C. CMR A'B' vuông góc với A'C'.
2. Cho tam giác ABC cân ở A. Kẻ tia phân giác BD của góc B và tia phân giác DM của góc BDC, đường phân giác của góc ADB cắt đường thẳng BC tại N. CMR BD = 1/2 MN.
3. Từ đỉnh A của tam giác ABC, kẻ các đường vuông góc xuống các tia phân giác trong và ngoài của các góc tại đỉnh B và C. CMR chân các đường vuông góc đó thẳng hàng.
cho tam giác ABC vuông tại A . Kẻ AH vuông góc với BC , Tia phân giác của góc HAB cắt Bc ở D . Tia phân giác của góc HAC cắt BC ở E.
a) Chứng Minh các tam giác ABE và ACD là tam giác cân
b) gọi I là giao điểm của các tia phân giác của tam giác ADE
nhầm ấn lộn xíu !
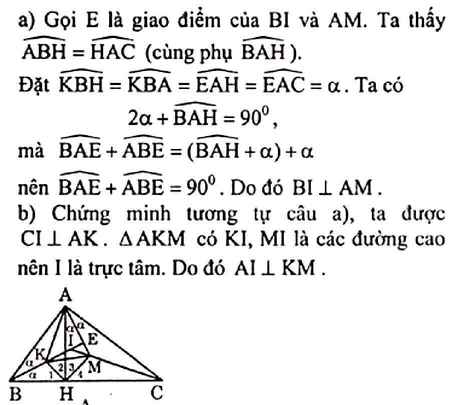
Xét tam giác ABH ta có: ABH + BAH = 90
=> BAE + ABH = BAE + 90 - BAH = BAE - BAH + 90 = HAE + 90
Xét tam giác AHE ta có góc ngoài là AEC có số đo là HAE + 90
Mà ta thấy BAE + ABH là số đo cũng của góc ngoài AEC của tam giác ABE
=> BAE + ABH = HAE + 90
=>... tự làm
Xem thêm câu trả lời
cho tam giác ABC vuông tại A . Kẻ AH vuông góc với BC , Tia phân giác của góc HAB cắt Bc ở D . Tia phân giác của góc HAC cắt BC ở E.
a) Chứng Minh các tam giác ABE và ACD là tam giác cân
b) gọi I là giao điểm của các tia phân giác của tam giác ADE
a: \(\widehat{BEA}+\widehat{EAH}=90^0\)
\(\widehat{BAE}+\widehat{CAE}=90^0\)
mà \(\widehat{HAE}=\widehat{CAE}\)
nên \(\widehat{BEA}=\widehat{BAE}\)
hay ΔABE cân tại B
\(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{CDA}+\widehat{HAD}=90^0\)
mà \(\widehat{BAD}=\widehat{HAD}\)
nên \(\widehat{CAD}=\widehat{CDA}\)
hay ΔDCA cân tại C
b: Đề bài yêu cầu gì?
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC. tia phân giác của góc HAB cắt BC ở D, tia phân giác của HAC cắt BC ở E. Chứng minh rằng: giao điểm các đường phân giác của tam giác ABC là giao điểm các đường trung trực của tam giác ADE.
B1: Cho tam giác ABC có góc C bằng 30 độ. Tia phân giác của góc B và đường phân giác góc ngoài tại A cắt nhau ở E. Tính số đo góc BCEB2: Cho tam giác ABC có I là giao điểm các tia pg của góc B và góc C. Gọi D là giao điểm của AI và BC. Kẻ IH vuông góc BC (H thuộc BC) CMR: góc BIH góc CIDB3: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. (H thuộc BC), các tia pg của góc HAC và AHC cắt nhau ở I. Tia phân giác của góc HAB cắt BC ở D. Cm: CI điq ua trung điểm của AD
Đọc tiếp
B1: Cho tam giác ABC có góc C bằng 30 độ. Tia phân giác của góc B và đường phân giác góc ngoài tại A cắt nhau ở E. Tính số đo góc BCE
B2: Cho tam giác ABC có I là giao điểm các tia pg của góc B và góc C. Gọi D là giao điểm của AI và BC. Kẻ IH vuông góc BC (H thuộc BC) CMR: góc BIH = góc CID
B3: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. (H thuộc BC), các tia pg của góc HAC và AHC cắt nhau ở I. Tia phân giác của góc HAB cắt BC ở D. Cm: CI điq ua trung điểm của AD
Cho tam giác ABC. Các tia phân giác trong và phân giác ngoài của góc C cắt đường thẳng AB lần lượt ở D và E. Tính góc CED theo góc A và góc B của tam giác ABCCho tam giác ABC vuông ở A. Kẻ đường cao AH, tia phân giác của góc A cắt BC tại D. Biết góc DAH=15 độ, tính các góc của tam giác ABCGIÚP MÌNH VỚI NHA MÌNH ĐANG CẦN GẤP
Xem chi tiết
Bài 1:
Vì CD và CE lần lượt là phân giác trong và phân giác ngoài của góc C nên \(CD\perp CE\)
Kẻ \(CH\perp AB\)thì \(\widehat{CED}=\widehat{HCD}\)cùng phụ với \(\widehat{EDC}\)
Ta có : \(\widehat{HCA}=90^0-\widehat{HAC}=90^0-\left[180^0-\widehat{BAC}\right]=\widehat{BAC}-90^0\)
\(\widehat{ACD}=\frac{1}{2}\widehat{ACB}=\frac{1}{2}\left[180^0-\widehat{ABC}-\widehat{BAC}\right]=90^0-\frac{1}{2}\left[\widehat{ABC}+\widehat{BAC}\right]\)
Do đó \(\widehat{HCD}=\widehat{HCA}+\widehat{ACD}=\frac{\widehat{BAC}-\widehat{ABC}}{2}\)nếu \(\widehat{BAC}>\widehat{ABC}\).
Nếu \(\widehat{BAC}< \widehat{ABC}\)thì \(\widehat{HCD}=\frac{\widehat{ABC}-\widehat{BAC}}{2}\)
Vậy \(\widehat{HCD}=\left|\frac{\widehat{BAC}-\widehat{ABC}}{2}\right|\).
2. Giả sử \(\widehat{B}>\widehat{C}\), ta có : \(\widehat{DAH}=\frac{\widehat{B}-\widehat{C}}{2}\)
Suy ra \(\widehat{B}-\widehat{C}=2\widehat{DAH}=2\cdot15^0=30^0\)
Mặt khác \(\widehat{B}+\widehat{C}=90^0\)từ đó suy ra \(\widehat{B}=60^0,\widehat{C}=30^0\)
Nếu \(\widehat{B}< \widehat{C}\)thì chứng minh tương tự,ta có \(\widehat{B}=30^0,\widehat{C}=60^0\)
P/S : Hình bài 1 chỉ mang tính chất minh họa nhé
Đúng 0
Bình luận (0)
Theo yêu cầu vẽ hình của bạn Hyouka :)
2.
:
Đúng 0
Bình luận (0)
Cách giải thích tại sao \(\widehat{DAH}=\frac{\widehat{B}-\widehat{C}}{2}\)?
Trường hợp điểm H nằm giữa B và D \((\widehat{B}>\widehat{C})\)
Trong hai tam giác vuông AHB và AHC vuông ở H theo tính chất tổng các góc của một tam giác,ta có :
\(\widehat{B}+\widehat{BAH}+\widehat{H}=180^0\)=> \(\widehat{B}=90^0-\widehat{BAH}\)
\(\widehat{C}+\widehat{CAH}+\widehat{H}=180^0\)=> \(\widehat{C}=90^0-\widehat{CAH}\)
Vậy \(\widehat{B}-\widehat{C}=\widehat{CAH}-\widehat{HAB}(1)\)
Vì điểm H nằm giữa hai điểm B và D nên AD là tia phân giác của góc BAC nên \(\widehat{DAB}=\widehat{DAC}=\frac{\widehat{A}}{2}\)
, do đó \(\widehat{DAH}=\frac{\widehat{A}}{2}-\widehat{HAB}\). Lại có \(\widehat{DAH}=\widehat{HAC}-\widehat{DAC}=\widehat{HAC}-\frac{\widehat{A}}{2}\).
Từ đó suy ra \(2\widehat{DAH}=\widehat{HAC}-\widehat{HAB}\)hay \(\widehat{DAH}=\frac{\widehat{HAC}-\widehat{HAB}}{2}\) \((2)\)
Từ 1 và 2 suy ra \(\widehat{DAH}=\frac{\widehat{B}-\widehat{C}}{2}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, H là hình chiếu của A trên BC. Các tia phân giác của góc B và C cắt nhau tại I. Tia phân giác của góc AHB cắt BI ở K. Tia phân giác của góc AHC cắt CI ở M. Chứng minh rằng:
a/ BI vuông góc với AM.
b/ AI vuông góc với KM.
Nhanh giúp mình với ạ, vẽ cả hình được nữa thì càng tốt ạ
32. Cho O là 1 điểm nằm trong tam giác ABCa)Cmr góc BOCgóc BACb) Nếu O là giao điểm 2 tia phân giác của góc A và B, hãy cmr BOC là góc tù33. Tính các góc của tam giác ABC,biếta) 3 lần góc A4 lần góc B và A-B20 độb)góc B-góc C10 độ và góc C-góc A10 độ34. Cho tam giác ABC. Các tia phân giác trong và ngoài của góc C cắt đg thẳng AB lần lượt ở D và E. Tính góc CED theo góc A và góc B của tam giác ABC35. Cho tam giác ABC vuông ở A. Kẻ đg cao AH,tia phân giác của góc A cắt BC tại D. Biết góc DAH 15 độ...
Đọc tiếp
32. Cho O là 1 điểm nằm trong tam giác ABC
a)Cmr góc BOC>góc BAC
b) Nếu O là giao điểm 2 tia phân giác của góc A và B, hãy cmr BOC là góc tù
33. Tính các góc của tam giác ABC,biết
a) 3 lần góc A=4 lần góc B và A-B=20 độ
b)góc B-góc C=10 độ và góc C-góc A=10 độ
34. Cho tam giác ABC. Các tia phân giác trong và ngoài của góc C cắt đg thẳng AB lần lượt ở D và E. Tính góc CED theo góc A và góc B của tam giác ABC
35. Cho tam giác ABC vuông ở A. Kẻ đg cao AH,tia phân giác của góc A cắt BC tại D. Biết góc DAH= 15 độ, tính các góc của tam giác ABC
36. Cho tam giác ABC. Tia phân giác của góc A cắt BC ở D. Tính các góc của tam giác ABC, biết góc ADB=80 độ và góc B=1,5 lần góc C
Cho tam giác ABC vuông ở A. Các tia phân giác của góc B và C cắt nhau ở I. Kẻ IH vuông góc với BC ( H thuộc BC) Biết HI=1cm HB=2cm HC =3cm. Tính Cv tam giác ABC
bạn tự kẻ hình nhé
bl
vì H thuộc BC=>HB+HC=BC
mà HB=2cm .HC=3cm
=>BC=5cm
kẻ IK vuông góc AC;IF vuông góc AB
S tam giác BIC=(IH*BC):2=2,5
----------------AIC=(IK*AC):2
----------------AIB=(IF*AB):2
mà tam giác ABC chia thành 3 tam giác = nhau:AIB,AIC,ABC=>S tam giác ABC=2,5*3=7,5
Đáp số 7,5
Đúng 0
Bình luận (1)
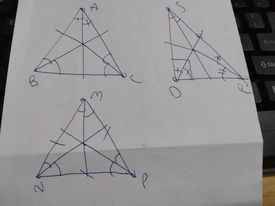
vẽ tam giác ABC cân ở A , vẽ các tia phân giác của các góc A, B, C . Vẽ tam giác DRS vuông tại D sau đó vẽ các tia phân giác của Các góc D, R, S. Vẽ tam giác MNP là tam giác đều . Sau đó vẽ các tia pg của các góc M, N, P