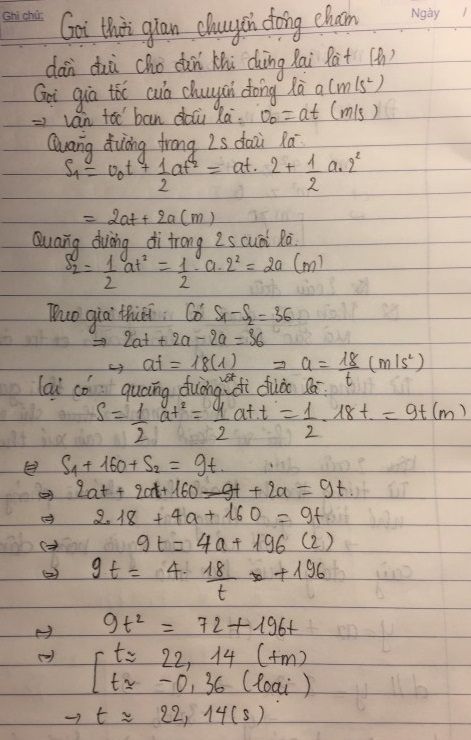Một xe chuyển động thẳng c/d đều, quãng đường xe đi được trong 2 s đầu dài hơn quãng đường xe đi được trong 2 s cuối là 36m, quãng đường giữa hia khoảng thời gian nói trên là 160m. Tìm thời gian chuyển động chậm dần đều cho đến khi dừng lại.

Những câu hỏi liên quan
Một xe chuyển động thẳng c/d đều, quãng đường xe đi được trong 2 s đầu dài hơn quãng đường xe đi được trong 2 s cuối là 36m, quãng đường giữa hia khoảng thời gian nói trên là 160m. Tìm thời gian chuyển động chậm dần đều cho đến khi dừng lại.
gọi t là thời gian xe đi hết quãng đường s
v=v0-a.t\(\Rightarrow\)v0=a.t
quãng đường đi với t thời gian là
s=v0.t-a.t2.0,5=a.t2-a.t2.0,5=0,5.a.t2
quãng đường đi được trong 2 giây đầu
s1=\(v_0.t_2-a.t_2^2.0,5\)\(\Rightarrow s_1=2at-2a\)
quãng đường đi được với t-2 giây đầu
s2=v0(t-2)-a.(t-2)2.0,5=\(0,5.t^2.a-2a\)
theo đề bài ta có
s2-s1=160m\(\Leftrightarrow0,5.t^2.a-2at\)=160 (1)
quãng đường đi được trong 2 giây cuối
s3=s-s2=2a
theo đề bài ta có
s1-s3=36m\(\Rightarrow\)2at-4a=36 (2)
từ (1),(2) giải hệ phương trình ta được
t=20s
vậy thời gian chuyển động chậm dần đến khi dừng lại là 20s
Đúng 0
Bình luận (3)
Một xe chuyển động thẳng c/d đều, quãng đường xe đi được trong 2 s đầu dài hơn quãng đường xe đi được trong 2 s cuối là 36m, quãng đường giữa hia khoảng thời gian nói trên là 160m. Tìm thời gian chuyển động chậm dần đều cho đến khi dừng lại.
Nhờ thầy cô cùng các bạn giải giúp. Em cảm ơn ạ.
Những bài toán như thế này thuộc kiểu bài toán giải bằng cách lập phương trình, hệ phương trình.
Gọi thời gian chuyển động chậm dần đều cho đến khi dừng lại là $t$
Gọi gia tốc của chuyển động là $a$
Suy ra vận tốc ban đầu là: $v_0=a.t$
Quãng đường trong 2s đầu là:
\(S_1=v_0t+\dfrac{1}{2}at^2=at.2+\dfrac{1}{2}a.2^2=2at+2a\)
Quãng đường đi trong 2s cuối là:
\(S_2=\dfrac{1}{2}at^2=\dfrac{1}{2}.a.2^2=2a\) (vì cuối cùng vật dừng lại nên ta áp dụng công thức ngược)
Theo giả thiết ta có: \(S_1-S_2=36\)
\(\Rightarrow 2at+2a-2a=36\)
\(\Rightarrow at =18\) (1)
Tổng quãng đường vật đã đi là: \(S=\dfrac{1}{2}at^2=\dfrac{1}{2}.at.t=\dfrac{1}{2}.18.t=9t\)
Theo giả thiết ta có: \(S=S_1+160+S_2\)
\(\Rightarrow 9t=2at+2a+160+2a\)
\(\Rightarrow 9t=2.18+4a+160\)
\(\Rightarrow 9t=4a+196\) (2)
Từ (1) suy ra \(a=\dfrac{18}{t}\), thay vào (2) ta được:
\(9t=\dfrac{4.18}{t}+196\)
\(\Rightarrow 9t^2-196t-72=0\)
\(\Rightarrow t \approx 22,14s\)
Đúng 0
Bình luận (6)
1. Một xe chuyển động thẳng nhanh dần đều qua 2 điểm A,B với các vận tốc vA=6m/s, vB=8m/s. Tính vận tốc tại trung điểm C của AB.
2. Một xe chuyển động thẳng chậm dần đều, quãng đường đi được trong 2s đầu tiên hơn quãng đường đi được trong 2s cuối cùng là 36m. Biết quãng đường đi được giữa 2 khoảng thời gian kể trên là 160m. Tính thời gian chuyển động của xe.
Bạn học Trường THPT Trần Quốc Tuấn ah lớp 10A2 đúng ko
Đúng 0
Bình luận (0)
Bài 1
Tóm tắt: \(v_A=6\left(\dfrac{m}{s}\right);\\ v_B=8\left(\dfrac{m}{s}\right);\\ s_{AC}=s_{CB}\\ v_{tb}=?\)
Giải:
-Vận tốc trung bình là
ADCT: \(v_{tb}=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{v_A}+\dfrac{1}{v_B}\right)}=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{6}+\dfrac{1}{8}\right)}=\dfrac{48}{7}\approx6,86\left(\dfrac{m}{s}\right)\)
Đúng 0
Bình luận (0)
Xe ô tô khởi hành từ A bắt đầu chuyển động nhanh dần đều trên đường thẳng và đi được đoạn đường S trong 150 giây. Thời gian vật đi 3/4 quãng đường cuối là
A. 50s
B.25s
C. 75s
D. 100s
Chọn C.
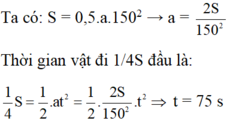
→ Thời gian vật đi 3/4 S cuối = 150 – 75 = 75 s.
Đúng 0
Bình luận (0)
Bài 1: Một xe chuyển động thẳng nhanh dần đều với vận tốc V0 và gia tốc a. Sau khi đi được quảng đường 10m thì có vận tốc là 5m/s, đi thêm quảng đường 37,5m thì vận tốc là 10m/s. Tính quãng đường xe đi được trong 20s.
Bài 2: Một xe chuyển động chậm dần đều: quảng đường xe đi được trong 2s đầu dài hơn quảng đường xe đi được trong 2s cuối là 36m. Uẳng đường giwuax 2 thời gian trên là 160m. Tính thời gian chuyển động chậm dần đều cho đến khi dừng lại.
Đọc tiếp
Bài 1: Một xe chuyển động thẳng nhanh dần đều với vận tốc V0 và gia tốc a. Sau khi đi được quảng đường 10m thì có vận tốc là 5m/s, đi thêm quảng đường 37,5m thì vận tốc là 10m/s. Tính quãng đường xe đi được trong 20s.
Bài 2: Một xe chuyển động chậm dần đều: quảng đường xe đi được trong 2s đầu dài hơn quảng đường xe đi được trong 2s cuối là 36m. Uẳng đường giwuax 2 thời gian trên là 160m. Tính thời gian chuyển động chậm dần đều cho đến khi dừng lại.
1) \(v^2-v_0^2=2as\)
=> \(5^2-v_0^2=2a.10\)
=> \(25-v_0^2=20a\) (1)
lại có: \(10^2-v_0^2=2a.47,5\)
=> \(100-v^2_0=95a\) (2)
từ (1) và (2) ta có hệ : \(\left\{{}\begin{matrix}25-v_0^2=20a\\100-v_0^2=95a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1m/s^2\\v_0=\sqrt{5}m/s\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Một ôtô chuyển động trên một quãng đường từ A đến B mất một khoảng thời gian t, vận tốc xe đi trong một nửa thời gian đầu là 42km/h, vận tốc xe đi trong nửa khoảng thời gian cuối là 60km/h. Tốc độ trung bình của ôtô trên cả quãng đường là:
A. 42km/h
B. 34km/h
C. 51km/h
D. 47km/h
Một xe chuyển động chậm dần đều: quãng đường xe đi dược trong 2s đầu dài hơn quãng đường ce đi trong 2s cuối là 36m, quãng đường giữa hai khoảng thời gian trên là 160m. Tìm thời gian chuyển động chậm dần đều đến khi dừng lại
Một xe khởi hành chuyển động thẳng chậm dần đều trên đoạn đường ABS. Đặt t1, v1 lần lượt là thời gian xe đi hết 1/4 quãng đường đầu tiên và vận tốc tức thời ở cuối quãng đường này. a) Thời gian xe đi hết 3/4 quãng đường còn lại tính theo t1 b) Vận tốc tức thời đạt được vào cuối cả đoạn đường tính theo v1M.n giải nhanh giùm nhak...camon rất nhìu nhá :D :)
Đọc tiếp
Một xe khởi hành chuyển động thẳng chậm dần đều trên đoạn đường AB=S. Đặt t1, v1 lần lượt là thời gian xe đi hết 1/4 quãng đường đầu tiên và vận tốc tức thời ở cuối quãng đường này.
a) Thời gian xe đi hết 3/4 quãng đường còn lại tính theo t1
b) Vận tốc tức thời đạt được vào cuối cả đoạn đường tính theo v1
M.n giải nhanh giùm nhak...camon rất nhìu nhá :D :)
Gọi \(v\) là vận tốc ban đầu của xe.
Suy ra:
\(v_1^2-v^2=2a\dfrac{S}{4}\Rightarrow (v_1-v)(v_1+v)=2a\dfrac{S}{4}\) (1)
\(v_1=v+at_1\Rightarrow v_1-v=at_1\) (2)
Thế (2) vào (1) ta được:
\(at_1.(v_1+v)=2a\dfrac{S}{4}\Rightarrow v=\dfrac{S}{2t_1}-v_1\)
Thế vào (2) ta được: \(2v_1-\dfrac{S}{2t_1}=a.t_1\Rightarrow a = \dfrac{2v_1}{t_1}-\dfrac{S}{2t_1^2}\)
Gọi \(v_2,t_2\) là vận tốc ở cuối đoạn đường và thời gian đi hết đoạn đường đó
Suy ra
\(v_2^2-v^2=2a.S\) (3)
\(v_2=v+at_2\) (4)
Bạn thế v và a ở trên vào PT (3) và (4) rồi tính tiếp nhé.
Đúng 0
Bình luận (2)
Cho một vật chuyển động thẳng đều trên quãng đường S mất thời gian t. Trong nửa thời gian đầu vật đi được 1/5 quãng đường S với tốc độ trung bình v1. Trên nửa quãng đường cuối vật đi trong 1/4 thời gian t với tốc độ trung bình v2. Hãy tính tốc độ trung bình trên cả quãng đường S biết v1+v2=60 m/s