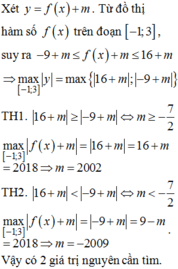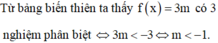cho hàm số f(x)=căn của 2x+3m , tìm m để hàm số trên xác định trên đoạn [1;3]

Những câu hỏi liên quan
Cho hàm số y = f(x) = (1- 3m)x. a) Tìm giá trị của m và xác định công thức của hàm số, biết đồ thị hàm số đi qua điểm ( -3 ; 24). b) Với công thức hàm số xác định được ở trên, tìm toạ độ của điểm A có hoành độ là 2 nằm trên đồ thị hàm số.
a: Thay x=-3 và y=24 vào y=(1-3m)x, ta được:
-3(1-3m)=24
=>-3+9m=24
=>m=3
Đúng 0
Bình luận (0)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{x+m}{x+1}\) nghịch biến trên từng khoảng xác định
b) \(y=\dfrac{2x-3m}{x-m}\) đồng biến trên từng khoảng xác định
a: TXĐ: D=R\{-1}
\(y'=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+1\right)'\left(x+m\right)}{\left(x+1\right)^2}\)
\(=\dfrac{x+1-x-m}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x+1\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\)
=>\(\dfrac{1-m}{\left(x+1\right)^2}< 0\)
=>1-m<0
=>m>1
b: TXĐ: D=R\{m}
\(y=\dfrac{2x-3m}{x-m}\)
=>\(y'=\dfrac{\left(2x-3m\right)'\left(x-m\right)-\left(2x-3m\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{2\left(x-m\right)-\left(2x-3m\right)}{\left(x-m\right)^2}=\dfrac{2x-2m-2x+3m}{\left(x-m\right)^2}\)
\(=\dfrac{m}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)
=>\(\dfrac{m}{\left(x-m\right)^2}>0\)
=>m>0
Đúng 0
Bình luận (0)
Cho hàm số y f(x) xác định trên
ℝ
-
1
;
1
,
liên tục trên từng khoảng xác định và có bảng biến thiên như sau:Tìm tất cả các giá trị thực của tham số của m để phương trình f(x) 3m có ba nghiệm phân biệt: A.
-
1
m
2
3
B.
m...
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ \ - 1 ; 1 , liên tục trên từng khoảng xác định và có bảng biến thiên như sau:
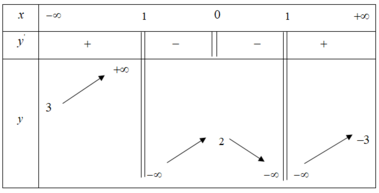
Tìm tất cả các giá trị thực của tham số của m để phương trình f(x) =3m có ba nghiệm phân biệt:
A. - 1 < m < 2 3
B. m < - 1
C. m ≤ - 1
D. m < - 3
Cho hàm số y f(x) xác định trên
ℝ
−
1
;
1
,
liên tục trên từng khoảng xác định và có bảng biến thiên như sau: Tìm tất cả các giá trị thực của tham số của m để phương trình f(x) 3m có ba nghiệm phân biệt: A.
−
1
m
2
3
....
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ \ − 1 ; 1 , liên tục trên từng khoảng xác định và có bảng biến thiên như sau:
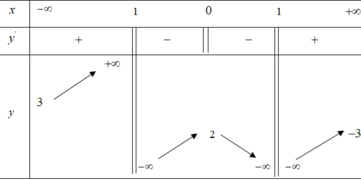
Tìm tất cả các giá trị thực của tham số của m để phương trình f(x) = 3m có ba nghiệm phân biệt:
A. − 1 < m < 2 3 .
B. m < − 1.
C. m ≤ − 1.
D. m < − 3.
Đáp án C
Dựa vào bảng biến thiên của đồ thị hàm số ⇒ f ( x ) = 3 m có 3 nghiệm phân biệt khi và chỉ khi 3 m ≤ − 3 ⇔ m ≤ − 1
Đúng 0
Bình luận (0)
Cho hàm số y f (x) xác định, liên tục trên đoạn [-1;4]. Hàm số y f’(x) có đồ thị trên đoạn [-1;4] như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số thực m để bất phương trình
f
x
-
m
≥
0
nghiệm đúng với mọi x thuộc đoạn
3
2
;
10
3
A.
m
≤...
Đọc tiếp
Cho hàm số y = f (x) xác định, liên tục trên đoạn [-1;4]. Hàm số y = f’(x) có đồ thị trên đoạn [-1;4] như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số thực m để bất phương trình f x - m ≥ 0 nghiệm đúng với mọi x thuộc đoạn 3 2 ; 10 3
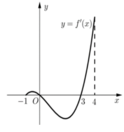
A. m ≤ f 3
B. m ≥ f 4
C. m ≤ f 3 2
D. m ≥ f 10 3
Cho hai hàm số yf(x) và yg(x) là các hàm xác định và liên tục trên R và có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là của đồ thị hàm số yf(x). Có bao nhiêu số nguyên m để phương trình f(1-g(2x-1))m có nghiệm thuộc đoạn
-
1
;
5
2
A. 8 B. 3 C. 6 D. 4
Đọc tiếp
Cho hai hàm số y=f(x) và y=g(x) là các hàm xác định và liên tục trên R và có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là của đồ thị hàm số y=f(x). Có bao nhiêu số nguyên m để phương trình f(1-g(2x-1))=m có nghiệm thuộc đoạn - 1 ; 5 2
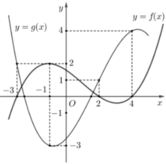
A. 8
B. 3
C. 6
D. 4
Có bao nhiêu giá trị nguyên của tham số m trên đoạn
[-2020; 2020] để hàm số f(x) = \(\dfrac{\sqrt{x^2-2x+3}}{x^2-2x+m-1}\) có tập xác định là R?
Cho hàm số y f(x) xác định và liên tục trên đoạn [-1;3] có đồ thị như hình vẽ sau. Có bao nhiêu giá trị của m để giá trị lớn nhất của hàm số
y
f
(
x
)
+
m
trên đoạn [-1;3] bằng 2018? A. 2. B. 4. C. 6 D. 0.
Đọc tiếp
Cho hàm số y= f(x) xác định và liên tục trên đoạn [-1;3] có đồ thị như hình vẽ sau.
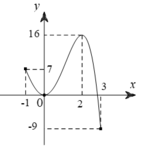
Có bao nhiêu giá trị của m để giá trị lớn nhất của hàm số y = f ( x ) + m trên đoạn [-1;3] bằng 2018?
A. 2.
B. 4.
C. 6
D. 0.
Cho hàm số yf(x) xác định và liên tục trên đoạn [-1;3] có đồ thị như hình vẽ sau.Có bao nhiêu giá trị của m để giá trị lớn nhất của hàm số y |f(x)+m| trên đoạn [-1;3] bằng 2018? A. 2. B. 4. C. 6 D. 0
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên đoạn [-1;3] có đồ thị như hình vẽ sau.
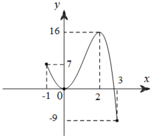
Có bao nhiêu giá trị của m để giá trị lớn nhất của hàm số y = |f(x)+m| trên đoạn [-1;3] bằng 2018?
A. 2.
B. 4.
C. 6
D. 0
Cho hàm số yf(x) xác định trên
ℝ
−
1
;
1
,
liên tục trên từng khoảng xác định và có bảng biên thiên sau Tìm tất cả các giá trị thực của tham số m sao cho phương trình f(x)3m có ba nghiệm phân biệt. A.
−
1
m
2
3
B.
m
−
1...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ \ − 1 ; 1 , liên tục trên từng khoảng xác định và có bảng biên thiên sau
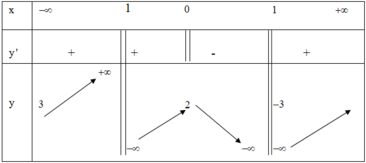
Tìm tất cả các giá trị thực của tham số m sao cho phương trình f(x)=3m có ba nghiệm phân biệt.
A. − 1 < m < 2 3
B. m < − 1
C. m ≤ - 1
D. m < - 3