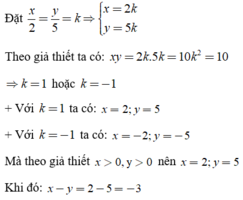(x-y)^2=10 và x.y=2 . tính x^2+y^2

Những câu hỏi liên quan
cho x+y=3 và x.y=-10 tính A= x^2+y^2 B= x^3+y^3
Ta có : \(A=x^2+y^2=x^2+2xy+y^2-2xy\)
\(A=\left(x+y\right)^2-2xy\)
Với \(x+y=3\) và \(xy=-10\)
\(\Rightarrow A=3^2-2.\left(-10\right)\)
\(A=9+20\)
\(A=29\)
Tương tự : \(B=x^3+y^3=\left(x+y\right)^3-3xy.\left(x+y\right)\)
\(B=\left(3\right)^3-3.\left(-10\right).3\)
\(B=117\)
Đúng 2
Bình luận (0)
Cho x/2 = y/5 và x.y = 10. Tính x - y, biết x > 0, y > 0
A. -3
B. 3
C. 8
D. -8
a)Cho x^2+y^2=2; x.y=1. Tính x+y và x-z
b) Cho x+y=5; x.y=2. Tính x^2+y^2 và x-y
Giúp mik zới.Thanks
\(\text{a) Ta có:}xy=1\Rightarrow\hept{\begin{cases}2xy=2\\-2xy=-2\end{cases}}\)
\(\text{Ta lại có: }x^2+y^2=2\Rightarrow\hept{\begin{cases}x^2+y^2+2xy=2+2=4\\x^2+y^2-2xy=2-2=0\end{cases}\Rightarrow\hept{\begin{cases}\left(x+y\right)^2=4\\\left(x-y\right)^2=0\end{cases}\Rightarrow}\hept{\begin{cases}x+y=\pm2\\x-y=0\end{cases}}}\)
\(\text{b) Ta có: }x+y=5\)
\(\Rightarrow\left(x+y\right)^2=25\)
\(\Rightarrow x^2+2xy+y^2=25\)
\(\Rightarrow x^2+4+y^2=25\)
\(\Rightarrow x^2+y^2=21\)
\(\text{b) Ta có: }x^2+y^2=21\)
\(\Rightarrow x^2-2xy+y^2=21-2xy\)
\(\Rightarrow\left(x-y\right)^2=21-4\)
\(\Rightarrow\left(x-y\right)^2=17\)
\(\Rightarrow x-y=\pm\sqrt{17}\)
Đúng 0
Bình luận (0)
Cho y,x là 2 số nguyên dương và x2+y2+10 chia het cho x.y. Cm (x2+y2+10): x.y chia het cho 4 và >=12. Giải giup mình
cho x,y thỏa mãn x+y=3 và x.y=10 tính giá trị các biểu thức sau
A=x2-2xy+y2
B=x^2+y^2
C=x^3+y^3
Ta có:
A=x2-2xy+y2+4xy-4xy
=(x+y)2-4xy
=9-40
=-31
B=x2+y2+2xy-2xy
=(x+y)2-2xy
=9-20
=-11
C=x3+y3
=(x+y)(x2-xy+y2)
=3.(-21)
=-63
Đúng 1
Bình luận (0)
1. Biết x+y=3 ; x.y=1. Tính x^2 =y^2;x^3 =y^3;x^4 =y^4
2. Biết x+y=4 ; x.y=2. Tính x^2 =y^2;x^3 =y^3;x^4 =y^4
Sửa đề: Các dấu bằng ở yêu cầu là dấu cộng.
1. Có: \(x+y=3\)
\(\Leftrightarrow\left(x+y\right)^2=3^2\)
\(\Leftrightarrow x^2+2xy+y^2=9\)
\(\Leftrightarrow x^2+y^2=9-2\cdot1=7\) (do \(xy=1\))
\(------\)
Lại có: \(x+y=3\)
\(\Leftrightarrow\left(x+y\right)^3=3^3\)
\(\Leftrightarrow x^3+y^3+3xy\left(x+y\right)=27\)
\(\Leftrightarrow x^3+y^3+3\cdot1\cdot3=27\) (do x + y = 3; xy = 1)
\(\Leftrightarrow x^3+y^3=18\)
Ta có: \(x^2+y^2=7\)
\(\Leftrightarrow\left(x^2+y^2\right)^2=7^2\)
\(\Leftrightarrow x^4+y^4+2\cdot\left(xy\right)^2=49\)
\(\Leftrightarrow x^4+y^4=49-2\cdot1=47\) (do xy = 1)
Đúng 0
Bình luận (1)
x-2/2=y-3/3 và x+y=10.khi đó x.y=..
cho y>x>0 và \(\frac{x^2+y^2}{x.y}=\frac{10}{3}\)Tính giá trị của biểu thức M=\(\frac{x-y}{x+y}\)
\(\frac{x^2+y^2}{xy}=\frac{10}{3}\Rightarrow3x^2+3y^2-10xy=0\)
\(\Rightarrow\left(3x^2-9xy\right)-\left(xy-3y^2\right)=0\Rightarrow3x\left(x-3y\right)-y\left(x-3y\right)=0\)
\(\Rightarrow\left(x-3y\right)\left(3x-y\right)=0\Rightarrow3x-y=0\left(y>x>0\Rightarrow x-3y< 0\right)\Rightarrow3x=y\)
\(M=\frac{x-y}{x+y}=\frac{x-3x}{x+3x}=\frac{-2x}{4x}=-\frac{1}{2}\)
Đúng 0
Bình luận (0)
Bài 1 : Tìm x
(x + 2 ) . ( x - 10)=13
Bài 2 : tính gtbt
A= 4.x + 4.y + x^3 . y^2+ x^2 . y^3 tai x + y = 7 ; x.y = 12