Đáp án D

Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu  (S) và mặt phẳng (P) sao cho KM lớn nhất

\(a+b=1\)

\(\Rightarrow a^2+2ab+b^2=1\)

\(\Rightarrow\left(a^2+b^2\right)+2ab=1\)

\(\Rightarrow2ab+2ab\le1\) (do \(a^2+b^2\ge2ab\))

\(\Rightarrow ab\le\dfrac{1}{4}\)

\(A=a\left(a^2+2b\right)+b\left(b^2-a\right)\)

\(=a^3+2ab+b^3-ab\)

\(=a^3+b^3+ab\)

\(=\left(a+b\right)^3-3ab\left(a+b\right)+ab\)

\(=1^3-3ab+ab=1-2ab\ge1-2.\dfrac{1}{4}=\dfrac{1}{2}\)

\(A_{min}=\dfrac{1}{2}\Leftrightarrow a=b=\dfrac{1}{2}\)

\(a+b=1\Rightarrow a=\dfrac{1}{2}+x;b=\dfrac{1}{2}+y\left(x+y=0\right)\)

có: \(A=a\left(a^2+2b\right)+b\left(b^2-a\right)=a^3+b^3+ab=a^2+b^2\\ =\left(\dfrac{1}{2}+x\right)^2+\left(\dfrac{1}{2}+y\right)^2=\dfrac{1}{2}+x^2+y^2\ge\dfrac{1}{2}\)

\(\Rightarrow A_{min}=\dfrac{1}{2}\Leftrightarrow x=y=0\Leftrightarrow a=b=\dfrac{1}{2}\)

2:

a: =>a^2+2ab+b^2-2a^2-2b^2<=0

=>-(a^2-2ab+b^2)<=0

=>(a-b)^2>=0(luôn đúng)

b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0

=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0

=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)

bài 5 nhé:

a) (a+1)²>=4a

<=>a²+2a+1>=4a

<=>a²-2a+1.>=0

<=>(a-1)²>=0 (luôn đúng)

vậy......

b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:

a+1>=\(2\sqrt{a}\)

tương tự ta có:

b+1>=\(2\sqrt{b}\)

c+1>=\(2\sqrt{c}\)

nhân vế với vế ta có:

(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)

<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)

<=>(a+)(b+1)(c+1)>=8 (vì abc=1)

vậy....

bạn nên viết ra từng câu

Chứ để như thế này khó nhìn lắm

bạn hỏi từ từ thôi

Ta có:

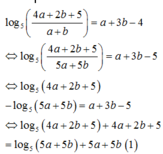
Xét hàm số

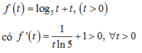
 Hàm số f t  đồng biến trên 0 ; + ∞

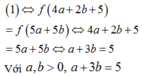
 ta có:

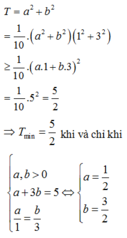
Chọn: D

Đáp án B

Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4  

⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b  

Xét hàm số f t = log 5 t + t t > 0 ⇒ f t  đồng biến trên 0 ; + ∞  

Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b  

⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2

a) Ta có: \(N=a^2+b^2+2a-b-\dfrac{1}{4}\)

\(=a^2+2a+1+b^2-b+\dfrac{1}{4}-\dfrac{3}{2}\)

\(=\left(a+1\right)^2+\left(b-\dfrac{1}{2}\right)^2-\dfrac{3}{2}\ge-\dfrac{3}{2}\forall a,b\)

Dấu '=' xảy ra khi a=-1 và \(b=\dfrac{1}{2}\)

a) Ta có: \(N=a^2+b^2+2a-b-\dfrac{1}{4}\)

\(=a^2+2a+1+b^2-b+\dfrac{1}{4}-\dfrac{3}{2}\)

\(=\left(a+1\right)^2+\left(b-\dfrac{1}{2}\right)^2-\dfrac{3}{2}\ge-\dfrac{3}{2}\forall a,b\)

Dấu '=' xảy ra khi a=-1 và \(b=\dfrac{1}{2}\)

Bài 2:

Ta có: M = a²+ab+b² -3a-3b-3a-3b +2001

=> 2M = ( a² + 2ab + b²) -4.(a+b) +4 + (a² -2a+1)+(b² -2b+1) + 3996

2M= ( a+b-2)² + (a-1)² +(b-1)² + 3996

=> Min_M = 1998 tại a=b=1

Câu 3: 

Ta có: P= x² +xy+y² -3.(x+y) + 3

=> 2P = ( x² + 2xy +y²) -4.(x+y) + 4 + (x² -2x+1) +(y² -2y+1)

2P = ( x+y-2)² +(x-1)²+(y-1)²

=> Min_P = 0 tại x=y=1

Bài1:

Ta có: a²+ b²+c²+d²= a.(b+c+d)

=> a²+b²+c²+d² -ab -ac -ad =0

=> 4a²+ 4b²+4c²+4d²-4ab -4ac -4ad=0

=> ( a² - 4ab +4b²) + ( a²- 4ac + 4c²) +( a² -4ad+ 4d²) + a²=0

=> ( a-2b)² + ( a-2c)² + (a-2d)² + a² =0

=> ....

KL: a=b=c=d=0