4cosx-3sinx=(m3-4m+3)x+m-4 tìm m để pt vô nghiệm.giúp với!!!!

Những câu hỏi liên quan
tìm m để bất pt \(\left(3sinx-4cosx\right)^2-6sinx+8cosx\ge2m-1\) có nghiệm đúng với mọi x thuộc R
đặt \(3sinx-4cosx=t\) đk \(-5\le t\le5\) pt trên trở thành \(t^2-2t\ge2m-1\)
\(\left(t-1\right)^2\ge2m\Leftrightarrow m\le0\)
Đúng 0
Bình luận (2)
Tìm m để các bất phương trình sau đúng với mọi x: (3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1 A. m 1 B. m 1 C. m 2 D. m ≤ 0
Đọc tiếp
Tìm m để các bất phương trình sau đúng với mọi x:
(3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1
A. m = 1
B. m > 1
C. m > 2
D. m ≤ 0
Đáp án D
Đặt t = 3sin x - 4cos x => -5 ≤ t ≤ 5 (dùng bất đẳng thức bunhiacopxki)
Ta có: y = (3sin x – 4cos x)2 – 6sin x + 8cos x
= t2 – 2t = (t – 2)2 -1
Do -5 ≤ t ≤ 5 => 0 ≤ (t – 2)2 ≤ 36 => min y = -1
Suy ra yêu cầu bài toán -1 ≥ 2m - 1 ⇔ m ≤ 0.
Đúng 0
Bình luận (0)
Tìm m để các bất phương trình
(
3
sin
x
-
4
cos
x
)
2
-
6
sin
x
+
8
cos
x
≥
2
m
-
1
đúng với mọi
x
∈
ℝ
A. m 0 B.
m
≤
0...
Đọc tiếp
Tìm m để các bất phương trình ( 3 sin x - 4 cos x ) 2 - 6 sin x + 8 cos x ≥ 2 m - 1 đúng với mọi x ∈ ℝ
A. m> 0
B. m ≤ 0
C. m < 0
D. m ≤ 1
Xét hàm số y= ( 3sinx – 4cosx )2 – 6sinx + 8cosx
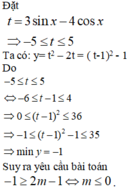
Đáp án B
Đúng 0
Bình luận (0)
Giải các pt lượng giác sau:
a, 4cosx - 3sinx = √5.sin2x + √10
b, 4cosx - 3sinx = √5.sin2x
c, 4cosx - 3sinx = -5
Mn giúp mình vs ạ :3
Có tất cả bao nhiêu tham số m đề phương trình sau vô nghiệm với ẩn x,
Tìm điều kiện của m để phương trình
3
sin
x
+
4
cos
x
m
có nghiệm.
Đọc tiếp
Tìm điều kiện của m để phương trình 3 sin x + 4 cos x = m có nghiệm.
![]()
![]()
![]()
![]()
38.Tìm giá trị lớn nhất nhỏ nhất của hàm số y=3(3sinx+4cosx)\(^2\)+4(3sinx+4cosx)+1
Lời giải:
Đặt \(3\sin x+4\cos x=t\)
Áp dụng BĐT Bunhiacopxky:
\(t^2=(3\sin x+4\cos x)^2\leq (3^2+4^2)(\sin ^2x+\cos ^2x)=25\)
\(\Rightarrow -5\leq t\leq 5\)
Với $t\in [-5;5]$ ta có:
\(y=3t^2+4t+1\leq 3.25+4.5+1=96\)
Mặt khác: \(y=3t^2+4t+1=3(t+\frac{2}{3})^2-\frac{1}{3}\)
\((t+\frac{2}{3})^2\geq 0, \forall t\in [-5;5]\Rightarrow y\geq -\frac{1}{3}\)
Vậy \(y_{\min}=\frac{-1}{3}; y_{\max}=96\)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị tham số m để hàm số sau chỉ nhận giá trị dương:
y=(3sinx - 4cosx)2 - 3sinx + 4cosx + m
Đặt \(t=3sinx-4cosx=5\left(\frac{3}{5}sinx-\frac{4}{5}cosx\right)=5sin\left(x-a\right)\)
\(\Rightarrow-5\le t\le5\)
\(\Rightarrow y=t^2-t+m\)
\(y>0\) ; \(\forall m\Leftrightarrow t^2-t+m>0\Leftrightarrow m>-t^2+t\) ; \(\forall m\)
\(\Leftrightarrow m>\max\limits_{\left[-5;5\right]}\left(-t^2+t\right)\)
Mà \(-t^2+t=-\left(t-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\)
\(\Rightarrow m>\frac{1}{4}\)
Đúng 0
Bình luận (0)
Tìm GTNN và GTLN (nếu có) của các hàm số sau:
1, y=sin6x +cos6x
2, y=\(\sqrt{4-cos^{2^{ }}3x}\) +1
3, y= 3(3sinx +4cosx )2 +4(4cosx +3sinx ) +1











