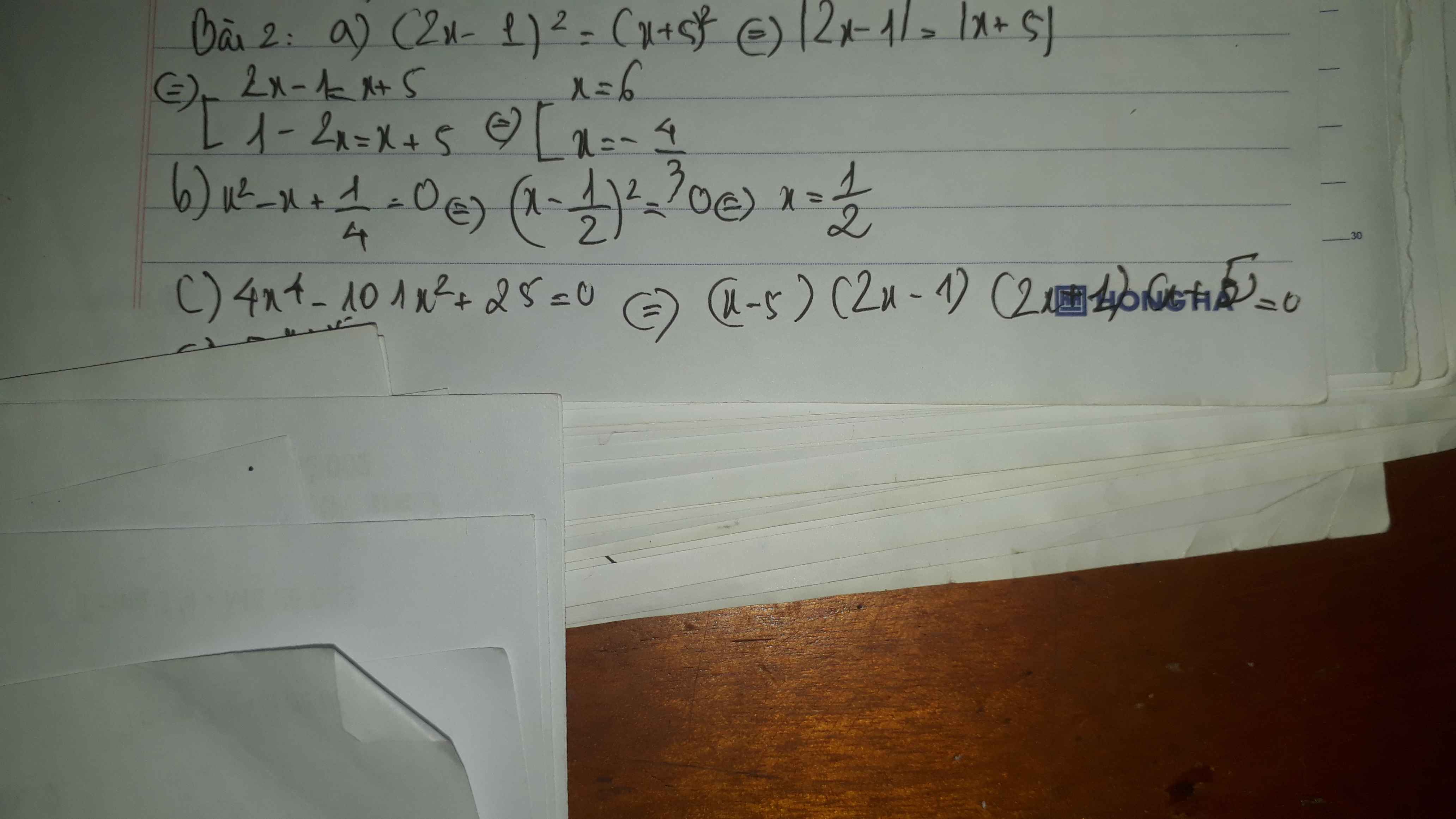Tìm GTLN:
a) A = 100 - 2x - x2
b) B = -3x2 + x
c) C = 3x(1 - x)

Những câu hỏi liên quan
Bài 13. Cho 2 đa thức: P(x)= 4x2 + x3 - 2x +3 -x-x3 +3x -2x2
Q(x)= 3x2 - 3x +2 -x3 +2x - x2
b)Tìm đa thức R(x) sao cho P(x) - Q(x) - R(x) =0
`P(x)=\(4x^2+x^3-2x+3-x-x^3+3x-2x^2\)
`= (x^3-x^3)+(4x^2-2x^2)+(-2x-x+3x)+3`
`= 2x^2+3`
`Q(x)=`\(3x^2-3x+2-x^3+2x-x^2\)
`= -x^3+(3x^2-x^2)+(-3x+2x)+2`
`= -x^3+2x^2-x+2`
`P(x)-Q(x)-R(x)=0`
`-> P(X)-Q(x)=R(x)`
`-> R(x)=P(x)-Q(x)`
`-> R(x)=(2x^2+3)-(-x^3+2x^2-x+2)`
`-> R(x)=2x^2+3+x^3-2x^2+x-2`
`= x^3+(2x^2-2x^2)+x+(3-2)`
`= x^3+x+1`
`@`\(\text{dn inactive.}\)
Đúng 1
Bình luận (1)
a: P(x)-Q(x)-R(x)=0
=>R(x)=P(x)-Q(x)
=2x^2+3+x^3-2x^2+x-2
=x^3+x+1
Đúng 1
Bình luận (0)
Bài 1: Thực hiện phép tính:
a) 2x.(3x + 3) b) 5x.(3x2-2x + 1) c) 3x2(2x +4)
d) 5x2.(3x2 + 4x – 1) e) (x-1).(2x +3) f) (x+2).(3x-5)
Bài 2: Tìm x, biết:
a) 3x(x+1) – 3x2 = 6
b) 3x(2x+1) – (3x +1).(2x-3) = 10
Bài 1:
\(a,=6x^2+6x\\ b,=15x^3-10x^2+5x\\ c,=6x^3+12x^2\\ d,=15x^4+20x^3-5x^2\\ e,=2x^2+3x-2x-3=2x^2+x-3\\ f,=3x^2-5x+6x-10=3x^2+x-10\)
Bài 2:
\(a,\Leftrightarrow3x^2+3x-3x^2=6\\ \Leftrightarrow3x=6\Leftrightarrow x=2\\ b,\Leftrightarrow6x^2+3x-6x^2+9x-2x-3=10\\ \Leftrightarrow10x=13\Leftrightarrow x=\dfrac{13}{10}\)
Đúng 3
Bình luận (0)
Bài 1: tìm GTLN hoặc GTNN của
a, N=-1-x-x2
b,B=3x2+4x-13
a) \(N=-1-x-x^2=-\left(x^2+x+\dfrac{1}{4}\right)-\dfrac{3}{4}=-\left(x+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}\)
\(maxN=-\dfrac{3}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
b) \(B=3x^2+4x-13=3\left(x^2+\dfrac{4}{3}x+\dfrac{4}{9}\right)-\dfrac{35}{3}=3\left(x+\dfrac{2}{3}\right)^2-\dfrac{35}{3}\ge-\dfrac{35}{3}\)
\(minB=-\dfrac{35}{3}\Leftrightarrow x=-\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
a: Ta có: \(N=-x^2-x-1\)
\(=-\left(x^2+x+1\right)\)
\(=-\left(x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)\)
\(=-\left(x+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{1}{2}\)
b: ta có: \(B=3x^2+4x-13\)
\(=3\left(x^2+\dfrac{4}{3}x-\dfrac{13}{3}\right)\)
\(=3\left(x^2+2\cdot x\cdot\dfrac{2}{3}+\dfrac{4}{9}-\dfrac{43}{9}\right)\)
\(=3\left(x+\dfrac{2}{3}\right)^2-\dfrac{43}{3}\ge-\dfrac{43}{3}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{2}{3}\)
Đúng 0
Bình luận (0)
Bài 1: Thực hiện phép tính:a) x(3x2 – 2x + 5) b) 1/3 x2 y2 (6x + 2/3x2 – y)c) ( 1/3x + 2)(3x – 6) d) ( 1/3x + 2)(3x – 6)e) (x2 – 3x + 1)(2x – 5) f) ( 1/2x + 3)(2x2 – 4x + 6)Bài 2: Tìm x, biết:a) 3(2x – 3) + 2(2 – x) –3 b) x(5 – 2x) + 2x(x – 1) 13c) 5x(x – 1) – (x + 2)(5x – 7) 6 d) 3x(2x + 3) – (2x + 5)(3x – 2) 8Bài 3: Chứng tỏ rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến: a) A x(2x + 1) – x2 (...
Đọc tiếp
Bài 1: Thực hiện phép tính:
a) x(3x2 – 2x + 5) b) 1/3 x2 y2 (6x + 2/3x2 – y)
c) ( 1/3x + 2)(3x – 6) d) ( 1/3x + 2)(3x – 6)
e) (x2 – 3x + 1)(2x – 5) f) ( 1/2x + 3)(2x2 – 4x + 6)
Bài 2: Tìm x, biết:
a) 3(2x – 3) + 2(2 – x) = –3 b) x(5 – 2x) + 2x(x – 1) = 13
c) 5x(x – 1) – (x + 2)(5x – 7) = 6 d) 3x(2x + 3) – (2x + 5)(3x – 2) = 8
Bài 3: Chứng tỏ rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến: a) A = x(2x + 1) – x2 (x + 2) + x3 – x + 3
b) B = (2x + 11)(3x – 5) – (2x + 3)(3x + 7) + 5
Bài 4: Tính giá trị của biểu thức
a) A = 2x( 1/2x2 + y) – x(x2 + y) + xy(x3 – 1) tại x = 10; y = – 1 10
b) B = 3x2 (x2 – 5) + x(–3x3 + 4x) + 6x2 tại x = –5
\(1,\\ a,=3x^3-2x^2+5x\\ b,=2x^3y^2+\dfrac{2}{9}x^4y^2-\dfrac{1}{3}x^2y^3\\ c,=x^2-2x+6x-12=x^2+4x-12\\ 2,\\ a,\Rightarrow6x-9+4-2x=-3\\ \Rightarrow4x=2\Rightarrow x=\dfrac{1}{2}\\ b,\Rightarrow5x-2x^2+2x^2-2x=13\\ \Rightarrow3x=13\Rightarrow x=\dfrac{13}{3}\\ c,\Rightarrow5x^2-5x-5x^2+7x-10x+14=6\\ \Rightarrow-8x=-8\Rightarrow x=1\\ d,\Rightarrow6x^2+9x-6x^2+4x-15x+10=8\\ \Rightarrow-2x=-2\Rightarrow x=1\)
Đúng 3
Bình luận (0)
\(3,\\ A=2x^2+x-x^3-2x^2+x^3-x+3=3\\ B=6x^2-10x+33x-55-6x^2-14x-9x-21=-76\)
Đúng 2
Bình luận (0)
Bài 4:
b: Ta có: \(B=3x^2\left(x^2-5\right)+x\left(-3x^3+4x\right)+6x^2\)
\(=3x^4-15x^2-3x^3+4x^2+6x^2\)
\(=-5x^2\)
\(=-5\cdot25=-125\)
Đúng 0
Bình luận (0)
Bài 9: Tìm x biết:
d) (2x - 1) . (3x + 1) + (3x + 4) . (3 - 2x) = 5
e) 0,6x (x - 0,5) - 0,3x (2x + 1,3) = 0,38
f) (c - 3x2)(x + 6) + x(3x2 + 17x) = 24
d: =>6x^2+2x-3x-1+9x-6x^2+12-8x=5
=>13=5(loại)
e: =>0,6x^2-0,3x-0,6x^2-0,39x=0,38
=>-0,69x=0,38
=>x=-38/69
Đúng 0
Bình luận (0)
Tìm GTLN hoặc GTLN:
a) `A = (5x^2 - 24x + 32)/(x^2 - 4x + 4)`
b) `B = ( 10x^2 + 24x + 15)/(x^2 + 2x + 1)`
\(A=\dfrac{4\left(x^2-4x+4\right)+\left(x^2-8x+16\right)}{x^2-4x+4}=4+\left(\dfrac{x-4}{x-2}\right)^2\ge4\)
\(A_{min}=4\) khi \(x=4\) (A max ko tồn tại)
\(B=\dfrac{6\left(x^2+2x+1\right)+\left(4x^2+12x+9\right)}{x^2+2x+1}=6+\left(\dfrac{2x+3}{x+1}\right)^2\ge6\)
\(B_{min}=6\) khi \(x=-\dfrac{3}{2}\)
B max ko tồn tại
Đúng 2
Bình luận (0)
Tìm x, biết.a/ 3x + 2(5 – x) 0 b/ x(2x – 1)(x + 5) – (2x2 + 1)(x + 4,5) 3,5c/ 3x2 – 3x(x – 2) 36. d/ (3x2 – x + 1)(x – 1) + x2(4 – 3x) Bài 1: Tính chia: a) (6x5y2 - 9x4y3 + 15x3y4): 3x3y2 b) (2x3 - 21x2 + 67x - 60): (x - 5) c) (6x3 – 7x2 – x + 2) : (2x + 1) d) (x2 – y2 + 6x + 9) : (x + y + 3)
Đọc tiếp
Tìm x, biết.
a/ 3x + 2(5 – x) = 0 b/ x(2x – 1)(x + 5) – (2x2 + 1)(x + 4,5) = 3,5
c/ 3x2 – 3x(x – 2) = 36.
d/ (3x2 – x + 1)(x – 1) + x2(4 – 3x) =
Bài 1: Tính chia:
a) (6x5y2 - 9x4y3 + 15x3y4): 3x3y2 b) (2x3 - 21x2 + 67x - 60): (x - 5) ![]()
c) (6x3 – 7x2 – x + 2) : (2x + 1) d) (x2 – y2 + 6x + 9) : (x + y + 3)
a: =>3x+10-2x=0
hay x=-10
c: \(\Leftrightarrow3x^2-3x^2+6x=36\)
=>6x=36
hay x=6
Đúng 1
Bình luận (0)
Bài 7. Tìm x,biết:
a) x-3x2=0 e) 5x(3x-1)+x(3x-1)-2(3x-1)=0
b) (x+3)2-x(x-2)=13 c) (x-4)2-36=0
d) x2-7x+12=0 g) x2-2018x-2019=0
Bài 8. Tìm x, biết
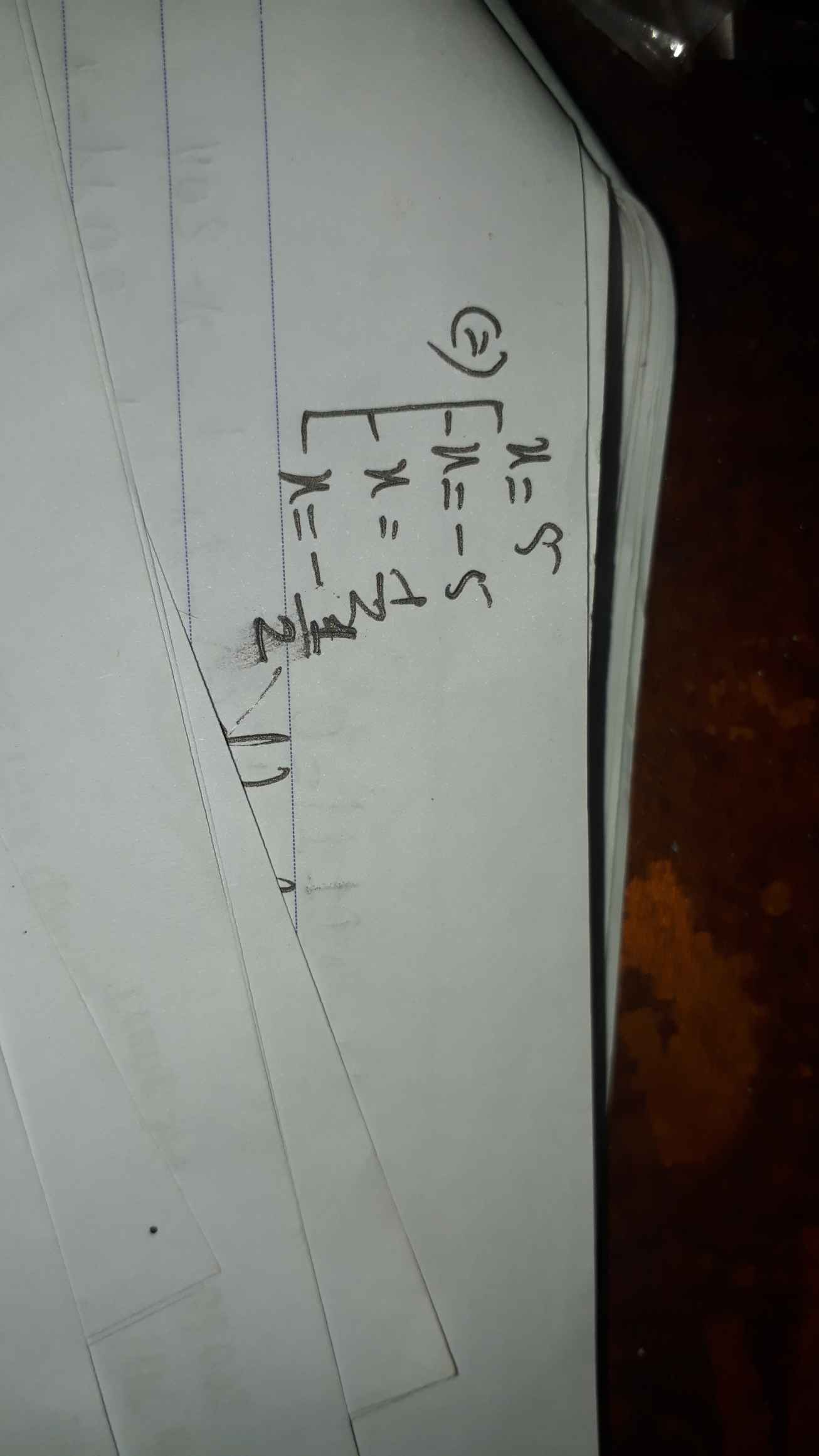
a) (2x-1)2=(x+5)2 b) x2-x+1/4
c) 4x4-101x2+25=0 d) x3-3x2+9x-91=0
Bài1: Thực hiện phép tính a) 2x(3x2 – 5x + 3) b) - 2x ( x2 + 5x+3) Bài 4: Tìm x, biết.a/ 3x + 2(5 – x) 0 b/ x(2x – 1)(x + 5) – (2x2 + 1)(x + 4,5) 3,5c/ 3x2 – 3x(x – 2) 36.II. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ Bài1: Phân tích đa thức thành nhân tử.a/ 14x2y – 21xy2 + 28x2y2 b/ x(x + y) – 5x – 5y.c/ 10x(x – y) – 8(y – x). d/ (3x + 1)2 – (x + 1)2e/ 5x2 – 10xy + 5y2 – 20z2. f/ x2 + 7x – 8g/ x3 – x + 3x2y + 3xy2 + y3 – y h/ x2 + 4x + 3.
Đọc tiếp
Bài1: Thực hiện phép tính
a) 2x(3x2 – 5x + 3) b) - 2x ( x2 + 5x+3)
Bài 4: Tìm x, biết.
a/ 3x + 2(5 – x) = 0 b/ x(2x – 1)(x + 5) – (2x2 + 1)(x + 4,5) = 3,5
c/ 3x2 – 3x(x – 2) = 36.
II. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
Bài1: Phân tích đa thức thành nhân tử.
a/ 14x2y – 21xy2 + 28x2y2 b/ x(x + y) – 5x – 5y.
c/ 10x(x – y) – 8(y – x). d/ (3x + 1)2 – (x + 1)2
e/ 5x2 – 10xy + 5y2 – 20z2. f/ x2 + 7x – 8
g/ x3 – x + 3x2y + 3xy2 + y3 – y h/ x2 + 4x + 3.
Bài 1:
a: \(=6x^3-10x^2+6x\)
b: \(=-2x^3-10x^2-6x\)
Bài 4:
a: =>3x+10-2x=0
=>x=-10
c: =>3x2-3x2+6x=36
=>6x=36
hay x=6
Đúng 0
Bình luận (0)
Bài 1:
\(a,=6x^3-10x^2+6x\\ b,=-2x^3-10x^2-6x\)
Bài 4:
\(a,\Leftrightarrow3x+10-2x=0\Leftrightarrow x=-10\\ b,\Leftrightarrow x\left(2x^2+9x-5\right)-\left(2x^3+9x^2+x+4,5\right)=3,5\\ \Leftrightarrow2x^3+9x^2-5x-2x^3-9x^2-x-4,5=3,5\\ \Leftrightarrow-6x=8\Leftrightarrow x=-\dfrac{4}{3}\\ c,\Leftrightarrow3x^2-3x^2+6x=36\Leftrightarrow x=6\)
Bài 1:
\(a,=7xy\left(2x-3y+4xy\right)\\ b,=x\left(x+y\right)-5\left(x+y\right)=\left(x-5\right)\left(x+y\right)\\ c,=\left(x-y\right)\left(10x+8\right)=2\left(5x+4\right)\left(x-y\right)\\ d,=\left(3x+1-x-1\right)\left(3x+1+x+1\right)\\ =2x\left(4x+2\right)=4x\left(2x+1\right)\\ e,=5\left[\left(x-y\right)^2-4z^2\right]=5\left(x-y-2z\right)\left(x-y+2z\right)\\ f,=x^2+8x-x-8=\left(x+8\right)\left(x-1\right)\\ g,\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\\ h,=x^2+3x+x+3=\left(x+3\right)\left(x+1\right)\)
Đúng 1
Bình luận (0)
1,chia:
a, ( 4x3- 19x+15): (2x- 3)
b, (5x4+ 9x3-2x2-4x-8) : ( x+1)
c, (5x3+14x2+3x+1) ; (x+2)
d,( x3+3x2+3x+1): (x+1)
2,tìm x để
(3x2+mx+27): (x+5)





















 Bài 1.
Bài 1.