Tìm các số a và bc thỏa mãn a nhân bc = 259, trong đó a ko=1 và các chữ số a, b, c không nhất thiết phải khác nhau.

Những câu hỏi liên quan
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0;1;2;3;4;5;6;7;8;9. Chọn ngẫu nhiên một số
a
b
c
¯
từ S. Tính xác suất để số được chọn thỏa mãn a
≤
bc
A
.
1
6
B
.
11
60
C
....
Đọc tiếp
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0;1;2;3;4;5;6;7;8;9. Chọn ngẫu nhiên một số a b c ¯ từ S. Tính xác suất để số được chọn thỏa mãn a ≤ bc
A . 1 6
B . 11 60
C . 13 6
D . 9 11
Chọn B
Số phần tử của không gian mẫu ![]()
Gọi biến cố A” Chọn được một số thỏa mãn ![]() ”.
”.
Vì mà nên trong các chữ số sẽ không có số 0.
TH1: Số được chọn có chữ số giống nhau có 9 số.
TH2: Số được chọn tạo bới hai chữ số khác nhau.
Số cách chọn ra 2 chữ số khác nhau từ 9 chữ số trên là: C 9 2 .
Mỗi bộ 2 chữ số được chọn tạo ra 2 số thỏa mãn yêu cầu.
Vậy có 2. C 9 2 số thỏa mãn.
TH3: Số được chọn tạo bởi ba chữ số khác nhau.
Số cách chọn ra 3 chữ số khác nhau từ 9 chữ số trên là: C 9 3 .
Mỗi bộ 3 chữ số được chọn chỉ tạo ra một số thỏa mãn yêu cầu.
Vậy có C 9 3 số thỏa mãn.
Vậy ![]()
Xác suất của biến cố A là: .
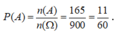
Đúng 0
Bình luận (0)
1/Cho a,b,c là các số nguyên khác 0 thỏa mãn ab - ac + bc - c2 = -1.Khi đó a/b = ?? (a phần b mà mik ko bik ghi phân số )
2/Tìm a,b nguyên khác 0 thỏa mãn a + b = ab
Xem thêm câu trả lời
Cho a, b, c là ba số khác 0 thỏa mãn: ab/a+b=bc/b+c=ca/c+a ( với giả thiết các tỉ số đều có nghĩa) và a+b=c=1 tính giá trị của biểu thức A=abc(a2+b2+c2)/ab+bc+ca
\(\dfrac{ab}{a+b}=\dfrac{bc}{b+c}=\dfrac{ca}{c+a}\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{c}+\dfrac{1}{a}\)
\(\Rightarrow\dfrac{1}{a}=\dfrac{1}{b}=\dfrac{1}{c}=\dfrac{1+1+1}{a+b+c}=\dfrac{3}{a+b+c}=\dfrac{3}{1}=3\)
\(\Rightarrow a=b=c=\dfrac{1}{3}\)
\(\Rightarrow A=\dfrac{a^3\left(a^2+b^2+c^2\right)}{a^2+b^2+c^2}=a^3=\left(\dfrac{1}{3}\right)^3=\dfrac{1}{27}\)
Đúng 0
Bình luận (0)
câu1:
a) Cho các số thực không âm a, b, c thỏa mãn a + b + c =1. Tìm giá trị lớn nhất và giá trị nhỏ
nhất của biểu thức:
P=\(\frac{ab+bc+ca-abc}{a+2b+c}\)
b) Cho các số thực a, b, c thỏa mãn \(^{a^2+b^2+c^2=1}\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P =ab +bc + ca .
Cho a,b,c là các số thực không âm thỏa mãn a+b+c=1.Tìm giá trị lớn nhất và nhỏ nhất của biểu thức Q=ac+bc-2022ab
\(Q=ac+bc-2022ab\le ac+bc=c\left(a+b\right)\le\dfrac{1}{4}\left(c+a+b\right)^2=\dfrac{1}{4}\)
\(Q_{max}=\dfrac{1}{4}\) khi \(\left\{{}\begin{matrix}a+b+c=1\\ab=0\\c=a+b\end{matrix}\right.\) \(\Leftrightarrow\left(a;b;c\right)=\left(0;\dfrac{1}{2};\dfrac{1}{2}\right);\left(\dfrac{1}{2};0;\dfrac{1}{2}\right)\)
\(Q=c\left(a+b\right)-2022ab\ge c\left(a+b\right)-\dfrac{1011}{2}\left(a+b\right)^2\)
\(Q\ge c\left(1-c\right)-\dfrac{1011}{2}\left(1-c\right)^2\)
\(Q\ge c\left(1-c\right)-\dfrac{1011}{2}c\left(c-2\right)-\dfrac{1011}{2}\)
\(Q\ge\dfrac{c\left(1011+1013\left(1-c\right)\right)}{2}-\dfrac{1011}{2}\ge-\dfrac{1011}{2}\)
\(Q_{min}=-\dfrac{1011}{2}\) khi \(\left(a;b;c\right)=\left(\dfrac{1}{2};\dfrac{1}{2};0\right)\)
Đúng 0
Bình luận (0)
1. Cho 4 chữ số 0,1,5 và 8,hãy thiết lập các số có 3 chữ số khác nhau thỏa mãn điều kiện :
a, Chia hết cho 6.
b, Chia hết cho 15.
2. Hãy tìm số tự nhiên nhỏ nhất có 7 chữ số nhỏ nhất khác nhau chia hết cho 5.
3. Hãy viết thêm vào bên phải và bên trái số 1996 mỗi bên một chữ số để được số chia hết cho 2,5 và 9.
Cho a,b,c là các số thực thỏa mãn: ab+bc+ca=abc và a+b+c=1.
CMR ít nhất một trong các số a,b,c phải bằng 1.
Gợi ý: Xét P=(a-1)(b-1)(c-1).
Từ giả thiết ta suy ra \(\hept{\begin{cases}abc-ab-bc-ac=0\\a+b+c-1=0\end{cases}}\)
\(\Rightarrow\left(abc-ab-bc-ac\right)+\left(a+b+c-1\right)=0\)
\(\Leftrightarrow\left(abc-ab\right)-\left(ac-a\right)-\left(bc-b\right)+\left(c-1\right)=0\)
\(\Leftrightarrow ab\left(c-1\right)-a\left(c-1\right)-b\left(c-1\right)+\left(c-1\right)=0\)
\(\Leftrightarrow\left(ab-a-b+1\right)\left(c-1\right)=0\)
\(\Rightarrow\left(a-1\right)\left(b-1\right)\left(c-1\right)=0\)
\(\Rightarrow\) Ít nhất một trong các số a;b;c phải bằng 1 (đpcm)
Đúng 0
Bình luận (0)
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0;1;2;3;4;5;6;7;8;9. Chọn ngẫu nhiên một số
a
b
c
¯
từ S. Tính xác suất để số được chọn thỏa mãn
a
≤
b
≤
c
A.
1
6
B.
11
60
C.
13
60...
Đọc tiếp
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0;1;2;3;4;5;6;7;8;9. Chọn ngẫu nhiên một số a b c ¯ từ S. Tính xác suất để số được chọn thỏa mãn a ≤ b ≤ c
A. 1 6
B. 11 60
C. 13 60
D. 9 11
có bao nhiêu số tự nhiên lớn hơn 4000 có 4 chữ số đc lập từ các số 1,2,5,7 nếu
a, các chữ số của số đó ko nhất thiết phải khác nhau
b, các chữ số của số đó khác nhau
gọi số đó là \(\overline{abcd}\) ở đó a,b,c,d thuộc {1,2,5,7}
a, để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng chữ số 5 hoặc 7.
vậy chữ số a có 2 cách chọn, chữ số b có 4 cách chọn
chữ số c có 4 cách chọn, d cũng có 4 cách chọn
suy ra có tất cả các chữ số ớn hơn 4000 là 2.4.4.4=128 số
b, để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng 5 hoặc 7
mà các chữ số khác nhau
suy ra b có 3 cách chọn, c có 2 cách chọn và d có 1 cách chọn
số các chữ số cần tìm là: 2.3.2.1=12 số
Đúng 1
Bình luận (0)
Xem thêm câu trả lời





















