Cho tứ giác ABCD có AB//CD biết A^ = 3D^
B^ - C^ = 30 độ
tính A^ B^ C^ D^
Những câu hỏi liên quan
Cho tứ giác ABCD , AB song song CD góc A = góc 3D , góc B – góc C = 30 độ
Tính góc A , B , C , D
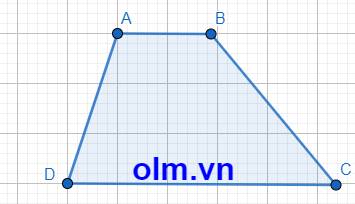
Vì AB//CD nên Góc A và góc D là hai góc trong cùng phía
\(\widehat{A}\)+ \(\widehat{D}\) = 1800 ⇒ \(\widehat{D}\) + 3\(\widehat{D}\) = 1800 ⇒ \(\widehat{D}\) = 1800:4 = 450
\(\widehat{A}\) = 450.3 =1350
\(\widehat{B}\)+\(\widehat{C}\) = 1800 ⇒ \(\widehat{B}\) + \(\widehat{B}\) - 300 = 1800 ⇒2\(\widehat{B}\) =2100 ⇒ \(\widehat{B}\) = 1050
\(\widehat{C}\) = 1050 - 300 = 750
Đúng 0
Bình luận (0)
cho tứ giác ABCD có góc A = 30 góc B = 2C (AB//CD) tính góc b,c,d
Ta có: Vì AB // CD
=> \(\widehat{D}=180^0-\widehat{A}=180^0-30^0=150^0\)
Vì \(\widehat{B}+\widehat{C}=180^0\Leftrightarrow2\widehat{C}+\widehat{C}=180^0\Leftrightarrow3\widehat{C}=180^0\)
\(\Rightarrow\widehat{C}=60^0\Rightarrow\widehat{B}=120^0\)
Tứ giác ABCD có AB//CD và A^= 3D^; B^-C^= 20°. Số đo các góc là A. A^= 135°;B^= 110°;C^= 70°;D^= 45°. B. A^= 145°;B^= 100°;C^= 80°;D^= 35°. C. A^= 155°;B^= 80°;C^= 60°;D^= 65°. D. A^= 135°;B^= 100°;C^= 80°;D^= 45°. Mong mọi người giúp tớ ah
Bài 3: Cho tứ giác ABCD có AB//CD và góc D =60 độ
a) Tính số đo góc A?
b) Biết góc B phần góc D = 4/5. Tính góc B, góc C
Bài 4: Cho tứ giác ABCD, góc A - góc B = 40 độ. Các tia phân giác của góc C, góc D cắt nhau tại O. Cho biết góc COD= 110 độ. Chứng minh rằng AB vuông góc với BC
Nhờ các bạn hướng dẫn mình hai bài này
a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.
Vì AB//CD, ta có góc ACD = góc BAD.
Vậy số đo góc A là 120 độ.
b) Gọi góc BCD là x độ.
Theo giả thiết, góc B phần góc D = 4/5, ta có:
góc B = (4/5) * góc D
= (4/5) * 60
= 48 độ.
Vì AB//CD, ta có góc BCD = góc BAD.
Vậy góc BAD = góc BCD = x độ.
Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.
Ta có: góc A + góc B + góc C + góc D = 360 độ.
Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:
120 + 48 + góc C + 60 = 360
góc C = 360 - 120 - 48 - 60 = 132 độ.
Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.
* Ib = bài 4
Đúng 0
Bình luận (0)
cho tứ giác ABCD có AB=a; BC=b; CD=c; DA=d (a,b,c,d > 0 thỏa \(a^2+b^2+c^2+d^2=\left(a+c\right)\left(b+d\right)\)
a) tứ giác ABCD có gì đặc biệt?
b) nếu cho thêm giả thiết AC*BD=ab+cd khi đó tính các góc của ABCD
a) \(a^2+b^2+c^2+d^2=ab+bc+ac+cd.\)
<=>\(2a^2+2b^2+2c^2+2d^2=2ab+2ac+2bc+2cd\)
<=>\(2a^2+2b^2+2c^2+2d^2-2ab-2bc-2ac-2cd=0\)
<=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)+\left(d^2-2cd+c^2\right)\)=0
<=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2+\left(d-c\right)^2=0\)
=>a=b=c=d
=> ABCD là hình thoi
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AB AD, CB CD (ta gọi tứ giác ABCD trong trường hợp này là tứ giác có hình cánh diêu).a) Chứng minh AC là đường trung trực của BD.b) Tính
B
^
,
D
^
b
i
ế
t
A
^
100
O
,
C
^
...
Đọc tiếp
Cho tứ giác ABCD có AB = AD, CB = CD (ta gọi tứ giác ABCD trong trường hợp này là tứ giác có hình cánh diêu).
a) Chứng minh AC là đường trung trực của BD.
b) Tính B ^ , D ^ b i ế t A ^ = 100 O , C ^ = 60 O
a) HS tự chứng minh
b) Sử dụng tổng bốn góc trong tứ giác và chú ý B ^ = D ^
Đúng 0
Bình luận (0)
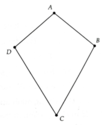
Tứ giác ABCD có AB = BC, CD = DA. Cho biết B = 100 0 , D = 70 0 , tính góc A và góc C.
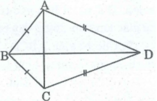
Xét ∆ BAD và ∆ BCD, ta có:
BA = BC (gt)
DA = DC (gt)
BD cạnh chung
Suy ra: ∆ BAD = ∆ BCD (c.c.c)
⇒ ∠ (BAD) = ∠ (BCD)
Mặt khác, ta có: ∠ (BAD) + ∠ (BCD) + ∠ (ABC) + ∠ (ADC) = 360 0
Suy ra: ∠ (BAD) + ∠ (BCD) = 360 0 – ( ∠ (ABC) + ∠ (ADC) )
2 ∠ (BAD) = 360 0 - 100 0 + 70 0 = 190 .
⇒ ∠ (BAD) = 190 0 : 2 = 95 0
⇒ ∠ (BCD) = ∠ (BAD) = 95 0
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có góc A = góc B = 90 độ
1) Chứng minh tứ giác ABCD là hình thang
Cho biết góc C = 3D Tính số đo góc C góc D
1)Cho hình thang cân ABCD (AB//CD)
Tính các góc của tứ giác biết:
a)A=3D
b)A=2C
2) Cho hình thang ABCD (AB//CD),AC cắt BD tại 0.
a)CMR:S tam giác ACD= S tam giác BCD
b)CMR:s tam giác AOD=S tam giác BOC
C)Cho S tam giác AOB=4 cm2,S tam giác COD=9 cm2.Tính S tam giác ABCD