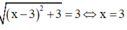f) (2x - 8)(4x + 16) = 0

<=> 2x - 8 = 0 hoặc 4x + 16 = 0

<=> 2x = 0 + 8 hoặc 4x = 0 - 16

<=> 2x = 8 hoặc 4x = -16

<=> x = 4 hoặc x = -4

g) 5x(6x - 12) = 0

<=> 5x = 0 hoặc 6x - 12 = 0

<=> x = 0 hoặc 6x = 0 + 12

<=> x = 0 hoặc 6x = 12

<=> x = 0 hoặc x = 2

h) 7(9 - x)(12 - 6x) = 0

<=> 9 - x = 0 hoặc 12 - 6x = 0

<=> -x = 0 - 9 hoặc -6x = 0 - 12

<=> -x = -9 hoặc -6x = -12

<=> x = 9 hoặc x = 2

ai làm có thưởng 2điem

Bài 1:

a) Ta có: 7x+12=0

\(\Leftrightarrow7x=-12\)

hay \(x=-\frac{12}{7}\)

Vậy: \(x=-\frac{12}{7}\)

b) Ta có: 5x-2=0

\(\Leftrightarrow5x=2\)

hay \(x=\frac{2}{5}\)

Vậy: \(x=\frac{2}{5}\)

c) Ta có: 12-6x=0

\(\Leftrightarrow6x=12\)

hay x=2

Vậy: x=2

d) Ta có: -2x+14=0

⇔-2x=-14

hay x=7

Vậy: x=7

Bài 2:

a) Ta có: 3x+1=7x-11

⇔3x+1-7x+11=0

⇔-4x+12=0

⇔-4x=-12

hay x=3

Vậy: x=3

b) Ta có: 2x+x+12=0

⇔3x+12=0

⇔3x=-12

hay x=-4

Vậy: x=-4

c) Ta có: x-5=3-x

⇔x-5-3+x=0

⇔2x-8=0

⇔2x=8

hay x=4

Vậy: x=4

d) Ta có: 7-3x=9-x

⇔7-3x-9+x=0

⇔-2x-2=0

⇔-2x=2

hay x=-1

Vậy: x=-1

e) Ta có: 5-3x=6x+7

⇔5-3x-6x-7=0

⇔-9x-2=0

⇔-9x=2

hay \(x=\frac{-2}{9}\)

Vậy: \(x=\frac{-2}{9}\)

f) Ta có: 11-2x=x-1

⇔11-2x-x+1=0

⇔12-3x=0

⇔3x=12

hay x=4

Vậy: x=4

g) Ta có: 15-8x=9-5

⇔15-8x=4

⇔8x=11

hay \(x=\frac{11}{8}\)

Vậy: \(x=\frac{11}{8}\)

Bài 3:

a) Ta có: 0,25x+1,5=0

⇔0,25x=-1,5

hay x=-6

Vậy: x=-6

b) Ta có: 6,36-5,2x=0

⇔5,2x=6,36

hay \(x=\frac{159}{130}\)

Vậy: \(x=\frac{159}{130}\)

a: \(3\left(x-3\right)-6x=0\)

=>\(3x-9-6x=0\)

=>-3x-9=0

=>3x+9=0

=>3x=-9

=>\(x=-\dfrac{9}{3}=-3\)

b: Đề thiếu vế phải rồi bạn

c: \(2\left(x-3\right)+3x=9\)

=>2x-6+3x=9

=>5x-6=9

=>5x=6+9=15

=>x=15/5=3

d: \(x\left(x-11\right)+2\left(x-11\right)=0\)

=>\(\left(x-11\right)\left(x+2\right)=0\)

=>\(\left[{}\begin{matrix}x-11=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-2\end{matrix}\right.\)

e: \(x\left(x+2\right)+8=x^2\)

=>\(x^2+2x+8=x^2\)

=>2x+8=0

=>2x=-8

=>x=-8/2=-4

f: \(8\left(x+1\right)+2x=-2\)

=>\(8x+8+2x=-2\)

=>10x=-2-8=-10

=>\(x=-\dfrac{10}{10}=-1\)

g: 12-3(x+2)=0

=>3(x+2)=12

=>x+2=12/3=4

=>x=4-2=2

a) Ta có: \(x^2-9x+20=0\)

\(\Leftrightarrow x^2-5x-4x+20=0\)

\(\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\)

\(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=4\end{matrix}\right.\)

Vậy: x∈{4;5}

b) Ta có: \(x^3-4x^2+5x=0\)

\(\Leftrightarrow x\left(x^2-4x+5\right)=0\)(1)

Ta có: \(x^2-4x+5\)

\(=x^2-4x+4+1=\left(x-2\right)^2+1\)

Ta có: \(\left(x-2\right)^2\ge0\forall x\)

\(\Rightarrow\left(x-2\right)^2+1\ge1>0\forall x\)

hay \(x^2-4x+5>0\forall x\)(2)

Từ (1) và (2) suy ra x=0

Vậy: x=0

c) Sửa đề: \(x^2-2x-15=0\)

Ta có: \(x^2-2x-15=0\)

\(\Leftrightarrow x^2+3x-5x-15=0\)

\(\Leftrightarrow x\left(x+3\right)-5\left(x+3\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left(x-5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=5\end{matrix}\right.\)

Vậy: x∈{-3;5}

d) Ta có: \(\left(x^2-1\right)^2=4x+1\)

\(\Leftrightarrow x^4-2x^2+1-4x-1=0\)

\(\Leftrightarrow x^4-2x^2-4x=0\)

\(\Leftrightarrow x\left(x^3-2x-4\right)=0\)

\(\Leftrightarrow x\left(x^3+2x^2+2x-2x^2-4x-4\right)=0\)

\(\Leftrightarrow x\cdot\left[x\left(x^2+2x+2\right)-2\left(x^2+2x+2\right)\right]=0\)

\(\Leftrightarrow x\cdot\left(x^2+2x+2\right)\cdot\left(x-2\right)=0\)(3)

Ta có: \(x^2+2x+2\)

\(=x^2+2x+1+1=\left(x+1\right)^2+1\)

Ta có: \(\left(x+1\right)^2\ge0\forall x\)

\(\Rightarrow\left(x+1\right)^2+1\ge1>0\forall x\)

hay \(x^2+2x+2>0\forall x\)(4)

Từ (3) và (4) suy ra

\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

Vậy: x∈{0;2}

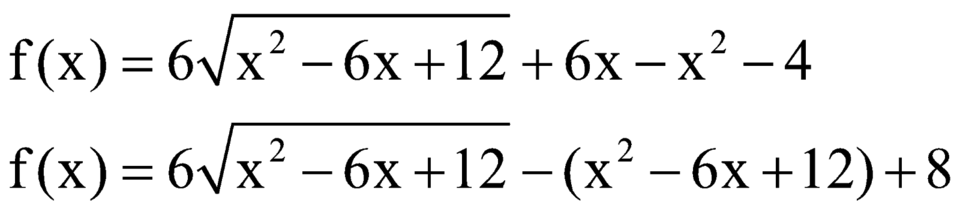
Đặt

 khi đó ta có

Ta có

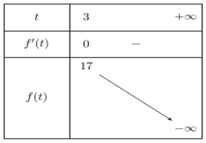
BBT:

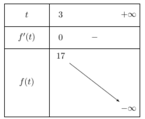
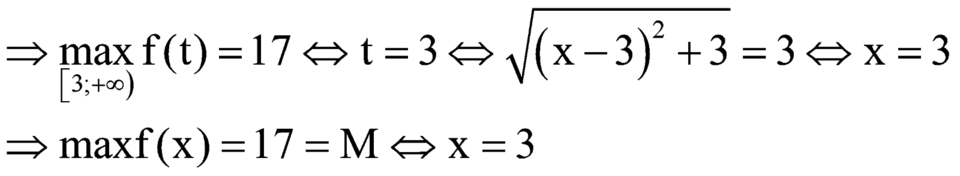
Vậy phương trình có nghiệm duy nhất x=3, do đó tích các nghiệm của chúng bằng 3.

Chọn B

\(a,x^3-3x^2+3x-1=0\)

\(\Leftrightarrow\left(x-1\right)^3=0\)

\(\Rightarrow x-1=0\Rightarrow x=1\)

\(b,\left(x-2\right)^3+6\left(x+1\right)^2-x+12=0\)

\(\Leftrightarrow x^3-6x^2+12x-8+6x^2+12x+6-x+12=0\)\(\Leftrightarrow x^3+23x+10=0\) (1)

Đặt \(t=\dfrac{x}{\dfrac{2\sqrt{69}}{3}}\Leftrightarrow x=\dfrac{2\sqrt{69}}{3}t\)

Khi đó: (1) \(\Leftrightarrow4t^3+3t=-0,2355375386\)

Đặt a= \(\sqrt[3]{-0,2355375386+\sqrt{-0,2355375386^2+1}}\)

Và \(\alpha=\dfrac{1}{2}\left(a-\dfrac{1}{a}\right)\) , ta được:

\(4\alpha^3+3\alpha=-0,2355375386\) , vậy \(t=\alpha\) là nghiệm của pt

Vậy t= \(\dfrac{1}{2}\left(\sqrt[3]{-0,2355375386}+\sqrt{-0,2355375386^2+1}\right)\) \(\left(\sqrt[3]{-0,2355375386-\sqrt{-0,2355375386^2+1}}\right)\)\(=-0,07788262891\)

\(\Rightarrow x=\dfrac{2\sqrt{69}}{3}.t=-0,4312944692\)

\(c,x^3+6x^2+12x+8=0\)

\(\Leftrightarrow\left(x+2\right)^3=0\)

\(\Leftrightarrow x+2=0\Rightarrow x=-2\)

\(d,x^3-6x^2+12x-8=0\)

\(\Leftrightarrow\left(x-2\right)^3=0\)

\(\Rightarrow x-2=0\Rightarrow x=2\)

\(e,8x^3-12x^2+6x-1=0\)

\(\Leftrightarrow\left(2x-1\right)^3=0\)

\(\Rightarrow2x-1=0\Rightarrow x=\dfrac{1}{2}\)

\(f,x^3+9x^2+27x+27=0\)

\(\Leftrightarrow\left(x+3\right)^3=0\)

\(\Rightarrow x+3=0\Rightarrow x=-3\)