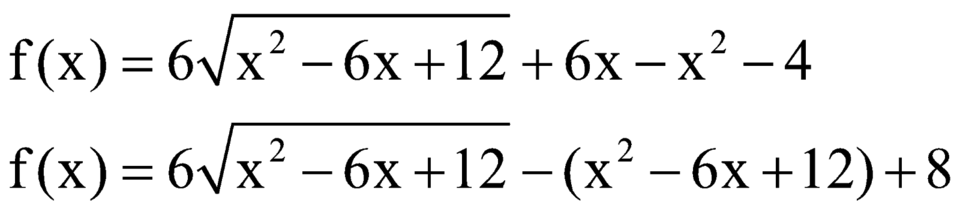
Đặt ![]()
khi đó ta có ![]()
Ta có ![]()
BBT:
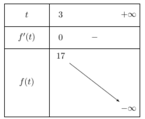
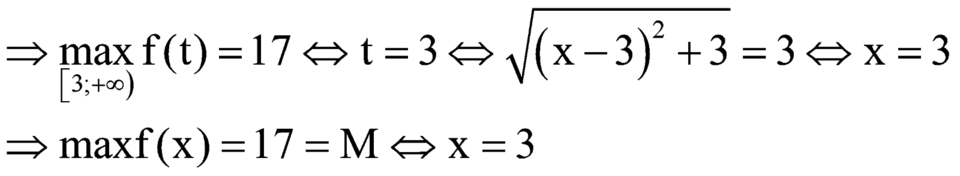
Vậy phương trình ![]() có nghiệm duy nhất x=3, do đó tích các nghiệm của chúng bằng 3.
có nghiệm duy nhất x=3, do đó tích các nghiệm của chúng bằng 3.
Chọn B
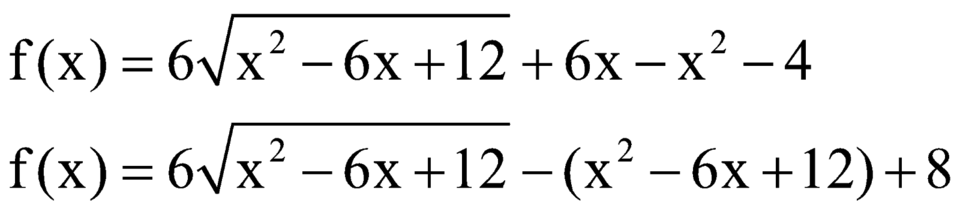
Đặt ![]()
khi đó ta có ![]()
Ta có ![]()
BBT:

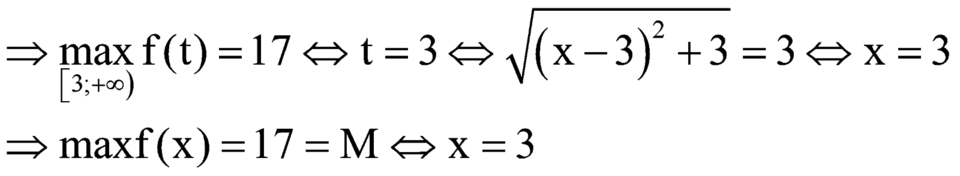
Vậy phương trình ![]() có nghiệm duy nhất x=3, do đó tích các nghiệm của chúng bằng 3.
có nghiệm duy nhất x=3, do đó tích các nghiệm của chúng bằng 3.
Chọn B
Gọi M là giá trị lớn nhất của hàm số f ( x ) = 6 x 2 - 6 x + 12 + 6 x - x 2 - 4 . Tính tích các nghiệm của phương trình f(x)=M.
A. -6
B. 3
C. -3
D. 6
Cho hàm số f(x)=x^2-4x+3. Có bao nhieu giá trị nguyên của tham số m để phương trình f^2(/x/)-(m-6)f(/x/)-m+5=0 có 6 nghiệm phân biệt
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)= x^3-3x^2+2 trên đoạn [-1,2] . Tính giá trị biểu thức P= M-2m A. 3√2-3 B. 2√2-5 C. 3√3-5 D. 3√3-3
Cho hai hàm số y=f(x),y=g(x) có đạo hàm là f'(x),g'(x) Đồ thị hàm số f'(x), g'(x) được cho như hinh vẽ dưới đây
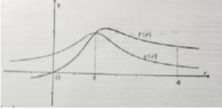
Biết rằng f(0)-f(6)<g(0)-g(6) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [0;6] lần lượt là:
A. h(6),h(2)
B. h(0),h(2)
C. h(2),h(6)
D. h(2),h(0)
Cho hàm số y = f ( x) có bảng biến thiên như hình dưới.
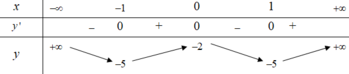
Số giá trị nguyên của tham số m để phương trình f x = m có 6 nghiệm phân biệt là
A. 3.
B. 0.
C. 2.
D. 1.
Cho hàm số y=f(x) thỏa mãn f ( 0 ) < 7 6 và có bảng biến thiên như sau:
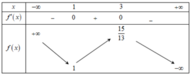
Giá trị lớn nhất của tham số m để phương trình e 2 f 3 ( x ) - 13 2 f 2 ( x ) + 7 f ( x ) - 1 2 = m có nghiệm trên đoạn [0;2] là:
A. e 2
B. e 15 13
C. e 4
D. e 3
hàm số y = f(x) có bảng biến thiên như hình dưới.
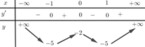
Số giá trị nguyên của tham số m để phương trình f x = m có 6 nghiệm phân biệt là
có 6 nghiệm phân biệt là
B. 0
C. 3
D. 1
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4