Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có thể):
e, E = -2x2 + 9x + 30
Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có thể):
d, \(D = -x^2 + 30x - 10\)
e, \(E = -2x^2 + 9x + 30\)
f, \(F = -5x^2 - 20x - 4\)
Toàn bộ đều tìm Max :)
D = -x2 + 30x - 10
D = -( x2 - 30x + 225 ) + 215
D = -( x - 15 )2 + 215
-( x - 15 )2 ≤ 0 ∀ x => -( x - 15 )2 + 215 ≤ 215
Đẳng thức xảy ra <=> x - 15 = 0 => x = 15
=> MaxD = 215 <=> x = 15
E = -2x2 + 9x + 30
E = -2( x2 - 9/2x + 81/16 ) + 321/8
E = -2( x - 9/4 )2 + 321/8
-2( x - 9/4 )2 ≤ 0 ∀ x => -2( x - 9/4 )2 + 321/8 ≤ 321/8
Đẳng thức xảy ra <=> x - 9/4 = 0 => x = 9/4
=> MaxE = 321/8 <=> x = 9/4
F = -5x2 - 20x - 4
F = -5( x2 + 4x + 4 ) + 16
F = -5( x + 2 )2 + 16
-5( x + 2 )2 ≤ 0 ∀ x => -5( x + 2 )2 + 16 ≤ 16
Đẳng thức xảy ra <=> x + 2 = 0 => x = -2
=> MaxF = 16 <=> x = -2
d) \(D=-x^2+30x-10\)
\(D=-\left(x^2-30x+10\right)\)
\(D=\left(x^2-30x+225-215\right)\)
\(D=-\left(x-15\right)^2+215\le215\)
Max D = 215 \(\Leftrightarrow x=15\)
e) \(E=-2x^2+9x+30\)
\(E=-2\left(x^2-\frac{9}{2}x-15\right)\)
\(E=-2\left(x-\frac{9}{4}\right)^2+\frac{321}{8}\le\frac{321}{8}\)
Max \(E=\frac{321}{8}\Leftrightarrow x=\frac{9}{4}\)
f) \(F=-5x^2-20x-4\)
\(F=-5\left(x^2+4x+\frac{4}{5}\right)\)
\(F=-5\left(x^2+4x+4+\frac{16}{5}\right)\)
\(F=-5\left(x+2\right)^2-16\le-16\)
Max F = -16 \(\Leftrightarrow x=-2\)
Hiệu của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x = 2 x 2 - ln x trên đoạn 1 e ; e là
![]()
![]()
![]()
![]()
Bài 2: Tìm giá trị nhỏ nhất, giá trị lớn nhất (nếu có) của:
a) A = x2 - 4x + 1
b) B = -x2 - 8x + 5
c) C = 2x2 - 8x +19
d) D = -3x2 - 6x +1
a) \(A=x^2-4x+1=\left(x-2\right)^2-3\ge-3\)
\(minA=-3\Leftrightarrow x=2\)
b) \(B=-x^2-8x+5=-\left(x+4\right)^2+21\le21\)
\(maxB=21\Leftrightarrow x=-4\)
c) \(C=2x^2-8x+19=2\left(x-2\right)^2+11\ge11\)
\(minC=11\Leftrightarrow x=2\)
d) \(D=-3x^2-6x+1=-3\left(x+1\right)^2+4\le4\)
\(maxD=4\Leftrightarrow x=-1\)
a) A = (x-2)^2 - 3 >= -3
--> A nhỏ nhất bằng -3
<=> x = 2
b) B = -(x+4)^2 + 21 <= 21
--> B lớn nhất bằng 21
<=> x = -4
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bạc hai y = -2x2 + 4x + 3
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = -3x2 + 2x + 1 trên (1;3)
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = x2 - 4x - 5 trên (-1;4)
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
Câu 3:
$y=x^2-4x-5$ có $a=1>0, b=-4; c=-5$ có trục đối xứng $x=\frac{-b}{2a}=2$
Do $a>0$ nên hàm nghịch biến trên $(-\infty;2)$ và đồng biến trên $(2;+\infty)$
Với $x\in (-1;4)$ vẽ BTT ta thu được $y_{\min}=f(2)=-9$
Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có thể):
\(K=\dfrac{-7}{-2x^2+8x-60}\)
\(L=\dfrac{8}{-3x^2+9x-40}\)
\(K=\frac{-7}{-2x^2+8x-60}\)
\(K=\frac{-7}{-2\left(x^2-4x+4-26\right)}\)
\(K=\frac{7}{2\left(x-2\right)^2-56}\)
Ta có : \(2\left(x-2\right)^2-56\ge-56\)
\(\Rightarrow K_{max}=\frac{-7}{56}\Leftrightarrow x=2\)
\(L=\frac{8}{-3x^2+9x-40}\)
\(L=\frac{8}{-3\left(x^2-3x+\frac{9}{4}+\frac{133}{12}\right)}\)
\(L=\frac{-8}{3\left(x-\frac{3}{2}\right)^2+\frac{133}{4}}\)
Ta có : \(3\left(x-\frac{3}{2}\right)^2+\frac{133}{4}\ge\frac{133}{4}\)
\(\Rightarrow L_{max}=-\frac{8.4}{133}=-\frac{32}{133}\Leftrightarrow x=\frac{3}{2}\)
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = l n ( 2 x 2 + e 2 ) trên [0;e]. Mệnh đề nào sau đây đúng
A. M + m = 5
B. M + m = 4 + ln3
C. M + m = 4 + ln2
D. M + m = 2 + ln3
Hãy vẽ đồ thị của các hàm số y = 2x2, y = -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:
Nếu a > 0 thì hàm số y = ax2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
Vẽ hình:
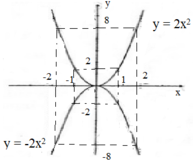
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
a)tìm giá trị nhỏ nhất của biểu thức E = |x-30|+|y-4|+(z-2018)^2
b)tìm giá trị lớn nhất của biểu thức F = 19-|x-5|-(y-2018)^2
Tìm các số nguyên x,y sao cho :
a, |x| - 2014 đạt giá trị nhỏ nhất
b, -|x| + 100 đạt giá trị lớn nhất
c, -18 + | x - 3 | đạt giả trị nhỏ nhất
d, Tìm giá trị lớn nhất của biểu thức: 2017 - |x + 3|
e, -|x - 30| - |y + 20| + 2018 đạt giá trị lớn nhất.