x^2 - y^2 + 7x - 7y
x^2*y^2+7x-7y PTNT giùm tôi với
Cho x-y=5. Tính S = x^2- 2xy + y^2 - 7x + 7y + 19
Solution:
\(S=x^2-2xy+y^2-7x+7y+19\)
\(S=\left(x-y\right)^2-7\left(x-y\right)+19\)
\(S=5^2-7\cdot5+19\)
\(S=9\)
Vậy...
Phân tích thành nhân tử x^2-y^2+7x-7y x^2-10x+25-9y^2
\(x^2-y^2+7x-7y=\left(x^2-y^2\right)+\left(7x-7y\right)=\left(x-y\right)\left(x+y\right)+7\left(x-y\right)=\left(x-y\right)\left(x+y+7\right)\)
\(x^2-10x+25-9y^2=\left(x^2-10x+25\right)-\left(3y\right)^2=\left(x-5\right)^2-\left(3y\right)^2=\left(x-3y-5\right)\left(x+3y-5\right)\)
\(x^2-y^2+7x-7y=\left(x-y\right)\left(x+y\right)+7\left(x-y\right)=\left(x-y\right)\left(x+y+7\right)\)
\(x^2-10x+25-9y^2=\left(x-5\right)^2-\left(3y\right)^2=\left(x-5-3y\right)\left(x-5+3y\right)\)
1. x2 - 10x + 25 - 9y2
<=> x2 - 10x + 52 - (3y)2
<=> (x - 5)2 - (3y)2
<=> (x - 5 - 3y)(x - 5 + 3y)
2. x2 - y2 + 7x - 7y
<=> (x - y)(x + y) + 7(x - y)
<=> (x + y + 7)(x - y)
Câu 15. Kết quả phân tích đa thức 6x 2 + 6xy + 7x + 7y thành nhân tử là :
A. (7x+y)(5x+y)
B. ( 3x +5 ) (x+y)
C. ( x+y ) ( 6x + 7)
D. ( 7x +6)( x + y)
x2y-xy2-7x+7y
Hệ phương trình x - y = 2 - 7 x + 7 y = 7 có nghiệm là:
A .S = {2;7 }
B .S = ∅
C .S= R
D .S= {2 }
Chọn đáp án B
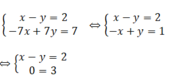
⇒ Hệ phương trình đã cho vô nghiệm ⇒ S = ∅
Cách 2: Ta thấy: 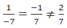 ⇒ Hệ pt vô nghiệm
⇒ Hệ pt vô nghiệm
phân tích đa thức thành nhân tử
a,x^2-xy-y^2 b,x^3+x^2+4 c,x^3-x^2-4 d,x^2-7x-y^2-7y
b: =x^3+2x^2-x^2+4
=x^2(x+2)-(x+2)(x-2)
=(x+2)(x^2-x+2)
c: =x^3-2x^2+x^2-4
=x^2(x-2)+(x-2)(x+2)
=(x-2)(x^2+x+2)
d: =(x-y)(x+y)-7(x+y)
=(x+y)(x-y-7)