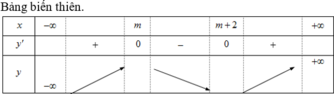
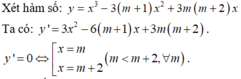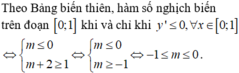Xác định m để: y = x3 - (m+2)x2 + (2m-3)x + 5 - 3m nghịch biến trên (-2;4) và (0;5)

Những câu hỏi liên quan
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hàm số y
(
m
-
1
)
x
3
+
(
m
-
1
)
x
2
-
(
2
m
+
1
)
+
5
nghịch biến trên tập xác định. A.
-
5
4
≤
m
≤
1
B....
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = ( m - 1 ) x 3 + ( m - 1 ) x 2 - ( 2 m + 1 ) + 5 nghịch biến trên tập xác định.
A. - 5 4 ≤ m ≤ 1
B. - 2 7 ≤ m < 1
C. - 7 2 ≤ m < 1
D. - 2 7 ≤ m ≤ 1
Chọn D.
Tập xác định: D = ℝ
Ta có ![]()
Xét m = 1, ta có y' = -3 < 0 ∀ x ∈ ℝ nên nghịch biến trên tập xác định.
Xét m ≠ 1 Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi
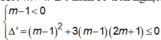
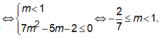
Vậy với - 2 7 ≤ m ≤ 1 thì hàm số y = ( m - 1 ) x 3 + ( m - 1 ) x 2 - ( 2 m + 1 ) + 5 nghịch biến trên tập xác định.
Đúng 0
Bình luận (0)
Xác định tham số m để hàm số sau:
a) 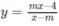 đồng biến trên từng khoảng xác định;
đồng biến trên từng khoảng xác định;
b) y = − x 3 + m x 2 − 3x + 4 nghịch biến trên.
a) Tập xác định: D = R \ {m}
Hàm số đồng biến trên từng khoảng ( - ∞ ; m), (m; + ∞ ) khi và chỉ khi:
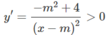
⇔ − m 2 + 4 > 0
⇔ m 2 < 4 ⇔ −2 < m < 2
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3 x 2 + 2mx – 3 ≤ 0
⇔ y′ = m 2 – 9 ≤ 0
⇔ m 2 ≤ 9 ⇔ −3 ≤ m ≤ 3
Đúng 0
Bình luận (0)
Xác định tham số m để hàm số sau: y = − x 3 + m x 2 − 3x + 4 nghịch biến trên.
Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3 x 2 + 2mx – 3 ≤ 0
⇔ y′ = m 2 – 9 ≤ 0
⇔ m 2 ≤ 9 ⇔ −3 ≤ m ≤ 3
Đúng 0
Bình luận (0)
Bài 1 : Định m để hàm số
1. Y=2x^3-3(2m+1)x^2 + 6m(m+1) Đồng biến trên khoảng (2; dương vô cùng)
2. Y= x^3+ (m-1)x^2 -(2m^2 +3m+2)x Nghịch biến trên (2; dvc)
Biết rằng S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y
x
3
- 3(m-1)
x
2
+ 3m(m+2)x nghịch biến trên đoạn [0;1]. Tính tổng các phần tử của S? A. S 0. B. S 1. C. S -2. D. S -1.
Đọc tiếp
Biết rằng S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y = x 3 - 3(m-1) x 2 + 3m(m+2)x nghịch biến trên đoạn [0;1]. Tính tổng các phần tử của S?
A. S = 0.
B. S = 1.
C. S = -2.
D. S = -1.
Với tất cả các giá trị thực nào của tham số m thì hàm số
y
x
3
-
3
(
m
+
1
)
x
2
+
3
m
(
m
+
2...
Đọc tiếp
Với tất cả các giá trị thực nào của tham số m thì hàm số y = x 3 - 3 ( m + 1 ) x 2 + 3 m ( m + 2 ) x nghịch biến trên đoạn [0;1]?
A. - 1 ≤ m ≤ 0
B. - 1 < m < 0
C. m ≥ - 1
D. m ≤ 0
Cho hàm số: y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5. Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+)
m
2
+ 5m = 0 ⇔ 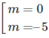
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
∆ ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
Đúng 0
Bình luận (0)
Xác định giá trị của tham số m để hàm số
y
x
2
+
m
+
1
x
-
1
2
-
x...
Đọc tiếp
Xác định giá trị của tham số m để hàm số y = x 2 + m + 1 x - 1 2 - x
nghịch biến trên mỗi khoảng xác định của nó
A. m = −1; B. m > 1;
C. m ∈ (−1;1); D. m ≤ −5/2.
Đáp án: D.
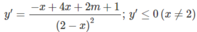
⇔ ∆ ′ = 2m + 5 ≤ 0
dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (- ∞ ; 2)
và (2; + ∞ ) khi m ≤ −5/2.
Đúng 0
Bình luận (0)