Tìm các giá trị của x để |x + 3| + |x + 1| = 3x

Những câu hỏi liên quan
Tìm các giá trị của x để biểu thức sau có giá trị bằng 2:
3
x
+
1
1
-
3
x
+
3
+
x
3
-
x
A. x 0 và
x
5
3...
Đọc tiếp
Tìm các giá trị của x để biểu thức sau có giá trị bằng 2:
3 x + 1 1 - 3 x + 3 + x 3 - x
A. x = 0 và x = 5 3
B. x = 0
C. x = 5 3
D. x = 1
Điều kiện: 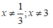
Để biểu thức đã cho có giá trị bằng 2 thì:
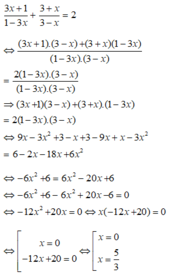
Kết hợp điều kiện phương trình đã cho có 2 nghiệm là x = 0 và x = 5 3
Chọn đáp án A
Đúng 0
Bình luận (0)
Tìm các giá trị của x để biểu thức sau có giá trị bằng 2:
3
x
+
1
1
-
3
x
+
3
+
x
3
-
x
A. x 0 và
x
5
3...
Đọc tiếp
Tìm các giá trị của x để biểu thức sau có giá trị bằng 2:
3 x + 1 1 - 3 x + 3 + x 3 - x
A. x = 0 và x = 5 3
B. x = 0
C. x = 5 3
D. x = 1
Điều kiện:
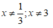
Để biểu thức đã cho có giá trị bằng 2 thì:
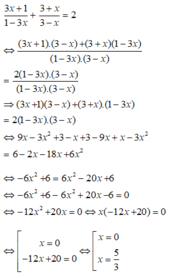
Kết hợp điều kiện phương trình đã cho có 2 nghiệm là x = 0 và x = 5 3
Chọn đáp án A
Đúng 0
Bình luận (0)
1. Tìm các giá trị nguyên của x để B nhận giá trị nguyên 2.Tìm các giá trị của x để B nhận giá trị nguyên 3. Tìm x biết : (căn x - 2).B + x - 3.căn x + căn 3 - 3x < hoặc bằng 0 B = căn x + 1/căn x - 2 Plsss làm ơn giúp t vs tớ ko bt làm mà cô này hay chửi t lắm huhu
tìm các giá trị của x để:|x+3|+|x+1|=3x
\(\left|x+3\right|+\left|x+1\right|=3x\)
\(\Leftrightarrow\left|x+3\right|=3x-\left|x+1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=3x-\left(x+1\right)\\x+3=3x-\left[-\left(x+1\right)\right]\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{2}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
tìm các giá trị của x để các biểu thức sau nhận giá trị âm
a) x2+5x
b) 3(2x+3) (3x-5)
bài 2. tìm các giá trị của x để biểu thức sau nhận giá trị dương
a)2y2-4y
b) 5(3y+1) (4y-3)
Bài 1:
a: \(x^2+5x=x\left(x+5\right)\)
Để biểu thức này âm thì \(x\left(x+5\right)< 0\)
hay -5<x<0
b: \(3\left(2x+3\right)\left(3x-5\right)< 0\)
\(\Leftrightarrow-\dfrac{3}{2}< x< \dfrac{5}{3}\)
Đúng 2
Bình luận (1)
Bài 2:
a: \(2y^2-4y>0\)
\(\Leftrightarrow y\left(y-2\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}y>2\\y< 0\end{matrix}\right.\)
b: \(5\left(3y+1\right)\left(4y-3\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}y>\dfrac{3}{4}\\y< -\dfrac{1}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
tìm các giá trị của x để : /x+3/+/x+1/=3x
tìm tất cả các giá trị nguyên của x để P= x^4+x^3-3x-1/x^2+x+1 nhận giá trị là số nguyên
\(P=\dfrac{x^4+x^3-3x-1}{x^2+x+1}=\dfrac{\left(x^2-1\right)\left(x^2+x+1\right)-2x}{x^2+x+1}=x^2-1-\dfrac{2x}{x^2+x+1}\)
Vì x \(\in Z\) nên để P \(\in Z\) thì : \(\dfrac{x}{x^2+x+1}\in Z\)
Đặt \(A=\dfrac{x}{x^2+x+1}\) . Với x = 0 ; ta có : \(P=-1\in Z\)
Với x khác 0 ; ta có : \(A=\dfrac{1}{x+\dfrac{1}{x}+1}\)
Nếu x > 0 ; ta có : \(0< A\le\dfrac{1}{3}\) ( vì \(x+\dfrac{1}{x}\ge2\) ) => Ko tồn tại g/t nguyên của A (L)
Nếu x < 0 ; ta có : \(x+\dfrac{1}{x}\le-2\) \(\Rightarrow x+\dfrac{1}{x}+1\le-1\)
Suy ra : \(0>A\ge\dfrac{1}{-1}=-1\) \(\Rightarrow A=-1\)
" = " \(\Leftrightarrow x+\dfrac{1}{x}=-2\Leftrightarrow x=-1\)
x = -1 ; ta có : P = 2 \(\in Z\) (t/m)
Vậy ...
Đúng 2
Bình luận (0)
Cho biểu thức Q = \(\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
a) rút gọn Q
b) Tính giá trị của Q khi x = \(4+2\sqrt{3}\)
c) Tìm các giá trị của x để Q = 3
d) Tìm các giá trị cảu x để Q > \(\dfrac{1}{2}\)
e) Tìm x \(\in\) Z để Q = Z
a: \(Q=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x-3\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
b: Khi x=4+2căn 3 thì \(Q=\dfrac{\sqrt{3}+1-2}{\sqrt{3}+1+2}=\dfrac{-3+2\sqrt{3}}{3}\)
c: Q=3
=>3căn x+6=căn x-2
=>2căn x=-8(loại)
d: Q>1/2
=>Q-1/2>0
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}-\dfrac{1}{2}>0\)
=>2căn x-4-căn x-2>0
=>căn x>6
=>x>36
d: Q nguyên
=>căn x+2-4 chia hết cho căn x+2
=>căn x+2 thuộc Ư(-4)
=>căn x+2 thuộc {2;4}
=>x=0 hoặc x=4(nhận)
Đúng 1
Bình luận (0)
tìm các giá trị của x,để các biểu thức sau có giá trị âm;
C =[3x-1]x[2x-1]
D=[2/3x-3]x[1/2x-1]


















