a, Hoành độ giao điểm tm pt 

\(\dfrac{x^2}{4}+m\left(x-1\right)-2=0\)

\(\Leftrightarrow x^2+4m\left(x-1\right)-8=0\)

\(\Leftrightarrow x^2+4mx-4m-8=0\)

\(\Delta'=4m^2-\left(-4m-8\right)=4m^2+4m+8=4\left(m^2+m\right)+2\)

\(=4\left(m+\dfrac{1}{2}\right)^2+1>0\)

Vậy pt luôn có 2 nghiệm pb 

hay (P) cắt (d) tại 2 điểm pb 

b, Theo Vi et \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{4m}{4}=-m\\x_Ax_B=\dfrac{-4m-8}{4}=-m-2\end{matrix}\right.\)

Ta có \(x_Ax_B\left(x_A+x_B\right)\)Thay vào ta được 

\(-m\left(-m-2\right)=m^2+2m+1-1=\left(m+1\right)^2-1\ge-1\)

Dấu ''='' xảy ra khi m = -1 

a: Phương trình hoành độ giao điểm là: \(x^2-mx+m-1=0\)

\(\Delta=\left(-m\right)^2-4\cdot\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\)

Để (P) cắt (d) tại hai điểm phân biệt thì m-2<>0

hay m<>2

b: \(\left|x_A-x_B\right|< 3\)

\(\Leftrightarrow\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}< 3\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2< 9\)

\(\Leftrightarrow m^2-4\left(m-1\right)< 9\)

\(\Leftrightarrow\left(m-2\right)^2-3< 0\)

=>(m+1)(m-5)<0

=>-1<m<5

Theo Cô si       4x+\frac{1}{4x}\ge24x+4x1​≥2  , đẳng thức xảy ra khi và chỉ khi   4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}4x=4x1​=1⇔x=41​). Do đó

                                         A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016A≥2−x+14x​+3​+2016

                                        A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014A≥4−x+14x​+3​+2014

                                        A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014A≥x+14x−4x​+1​+2014=x+1(2x​−1)2​+2014≥2014

Hơn nữa    A=2014A=2014 khi và chỉ khi \left\{{}\begin{matrix}x=\dfrac{1}{4}\\2\sqrt{x}-1=0\end{matrix}\right.{x=41​2x​−1=0​  \Leftrightarrow x=\dfrac{1}{4}⇔x=41​ .

Vậy  GTNN  =  2014

Phương trình hoành độ giao điểm:  x 2 − 2 x − 2 = x + m ⇔ x 2 − 3 x − 2 − m = 0

(d) cắt (P) tại hai điểm phân biệt A, B ⇔ Δ > 0 ⇔ 17 + 4 m > 0 ⇔ m > − 17 4

Giả sử (*) có hai nghiệm x 1 , x 2 thì x 1 + x 2 = − b a = 3 x 1 . x 2 = c a = − m − 2

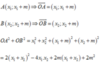
= 18 − 4 ( − 2 − m ) + 6 m + 2 m 2 = 2 m 2 + 10 m + 26 = 2 m + 5 2 2 + 27 2 ≥ 27 2 với m > − 17 4

Vậy giá trị nhỏ nhất của O A 2 + O B 2 là 27 2  khi m = − 5 2

Đáp án cần chọn là: A

Lời giải:

PT hoành độ giao điểm:

$2x^2-4x-m=0(*)$

Để 2 đths cắt nhau tại 2 điểm pb thì pt $(*)$ có 2 nghiệm $x_1,x_2$.

Điều này xảy ra khi $\Delta'=(-2)^2+2m>0\Leftrightarrow m> -2$

Áp dụng định lý Viet: 

$x_1+x_2=2$

$x_1x_2=\frac{-m}{2}$

Khi đó: $x_1^2+x_2^2=3$

$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=3$

$\Leftrightarrow 2^2-2.\frac{-m}{2}=3$

$\Leftrightarrow 4+m=3$

$\Leftrightarrow m=-1$ (tm)

a) Phương trình hoành độ giao điểm là:

\(x^2=2x-m+2\)

\(\Leftrightarrow x^2-2x+m-2=0\)

Để hai đồ thị hàm số chỉ có một điểm chung thì Δ=0

\(\Leftrightarrow4-1\cdot\left(m-2\right)=0\)

\(\Leftrightarrow m-2=4\)

hay m=6

PTHĐGĐ là:

x^2-(2m+1)x+m^2+m=0

Để (d) cắt (P) tại hai điểm phân biệt nằm về hai phía trục tung thì m^2+m<0

=>-1<m<0

a) pt hoành độ giao điểm: \(x^2-2x+3-m^2=0\) 

Để đường thẳng d cắt (P) tại 2 điểm phân biệt thì \(\Delta'>0\)

\(\Delta'=1+m^2-3\Rightarrow m^2-2>0\Rightarrow\left|m\right|>\sqrt{2}\)

b) Gọi giao điểm là \(A\left(x_1,y_1\right);B\left(x_2,y_2\right)\)

\(\Rightarrow A\left(x_1,x_1^2\right);B\left(x_2,x_2^2\right)\)

Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=3-m^2\end{matrix}\right.\)

Theo đề: \(y_1-y_2=8\Rightarrow x_1^2-x_2^2=8\Rightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)=8\)

\(\Rightarrow x_1-x_2=4>0\)

Ta có: \(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=4m^2-8\)

\(\Rightarrow x_1-x_2=\sqrt{4m^2-8}\left(x_1-x_2>0\right)\Rightarrow4=\sqrt{4m^2-8}\)

\(\Rightarrow4m^2-8=16\Rightarrow m=\pm\sqrt{6}\)