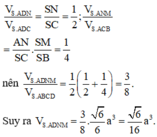cho hình chóp sabcd có đáy abcd là hình vuông cạnh a ,sa vuông góc với abcd. gọi m,n lầ lượt là trung điểm của sb và bc tính góc giữa mnd và abcd
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với đáy sa=a . gọi M,N lần lượt là trung điểm của SB và SD . Tính số đo góc giữa hai mặt phẳng (AMN) và (ABCD)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\) (1)
Tam giác SAB vuông cân tại A (do SA=SB=a)
\(\Rightarrow AM\perp SB\) (trung tuyến đồng thời là đường cao) (2)
(1);(2)\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow\left(SAC\right)\perp\left(AMN\right)\)
Từ A kẻ \(AH\perp SC\Rightarrow H\in\left(AMN\right)\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{HAC}\) là góc giữa (AMN) và (ABCD)
\(AC=a\sqrt{2}\) ; \(SC=a\sqrt{3}\)
\(sin\widehat{HAC}=cos\widehat{SCA}=\dfrac{AC}{SC}=\sqrt{\dfrac{2}{3}}\Rightarrow\widehat{HAC}\approx54^044'\)
Cho hình chóp SABCD có ABCD là hình vuông cạnh a, SA vuông góc với ABCD. Góc giữa SB ,(ABCD) = 60. Gọi M,N lần lượt là trung điểm của SB,SD. Tính khoảng cách giữa hai đường thẳng AN và CM?
Từ M kẻ MI//CN =>d(CN,MI)= d(C;SAD)= CD. Yếu tố góc 60 mình không biết có phải thừa hay ko?
bài mình được chữa đây. mn ai thích thì tham khảo nhé. Hay và khó ạ!
Sửa đề bài: d(AM,CN). MS=MD. NS=NB
SAD ΩSBC =PT. Kẻ TQ //AM. =>AM// (TCQ). d(AM,CN)=d(A, TCQ)
Từ T kẻ TH //SA. Từ H kẻ HK vuông với QC => QC vuông với THK. Kẻ HI vuông với TK => HI vuông với TCQ =>d (H, TCQ)= HI. Mặt #, \(\frac{d\left(A,TCQ\right)}{d\left(H,TCQ\right)}\)= \(\frac{AQ}{AH}\) => Tính HI => Có: TH= SA->Tính HK?
Có: QHK ∞ QDC. => \(\frac{HK}{CD}\) = \(\frac{QH}{QC}\)
QH= AD= AH=1/3QD.( Do PTHD là hcn=> PT= DH, có ST =AH(STAH: hbh) , PS= QH(PTAQ: hbh, ST=AH), PS= AD(PSAD:hbh, do M: TĐ SD, AP (SM=AM, SPA vuông tại S) ->PS=ST=AD=AH=HQ=> HK
Cho hình chóp Sabcd có sa vuông góc với abcd , đáy abcd là hình chữ nhật có cạnh ab=a, ad=2a , sa= 2a căn 3
Gọi I là trung điểm của ab , mặt phẳng P qua I và vuông góc với Sb . Tính góc giữa mặt phẳng Sb và mp abcd
Giups mìnhhh với các bạn ơii , mk cần lời giải chi tiết , cảm ơnn nhiềuuu ah
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với mp (ABCD), SD=a.căn 3. Gọi M và N lần lượt là hình chiếu của a lên SD và SB.
Tìm giao điểm K giữa SC và (AMN) và tính diện tích của MKNA
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với mp (ABCD), SD=a.căn 3. Gọi M và N lần lượt là hình chiếu của a lên SD và SB.
Tìm giao điểm K giữa SC và (AMN) và tính diện tích của MKNA
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 120 ° , SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng
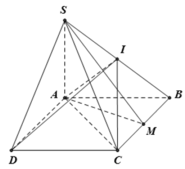
* Ta có SA ⊥ (ABCD) nên AM là hình chiếu của SM trên mặt phẳng (ABCD)
![]()
* ΔABCcó AB = BC = a ( vì ABCD là hình thoi) và ![]() nên ΔABC đều.
nên ΔABC đều.
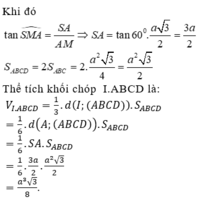
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 120°, SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng
A. a 3 6 4
B. a 3 3 8
C. a 3 3 2
D. a 3 3 6
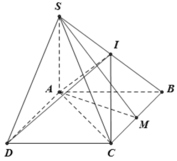
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật. AB=2a, AD= a√3 , SA vuông góc với đáy (ABCD). Gọi M là trung điểm CD. Góc giữa SM và đáy (ABCD) là 60 độ. Tính khoảng cách giữa hai đường thẳng AM và SB.
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, A B = B C = a , A D = 2 a , S A vuông góc với mặt đáy A B C D , S A = a . Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa MN và (SAC).
A. 2 5
B. 55 10
C. 3 5 10
D. 1 5
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 60 ° . Gọi M, N lần lượt là trung điểm của các cạnh SB, SC. Thể tích khối chóp S.ADNM bằng
A. 6 8 a 3
B. 3 6 16 a 3
C. 6 16 a 3
D. 6 24 a 3
Chọn đáp án C.
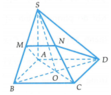
Gọi O là tâm của hình vuông ABCD thì B D ⊥ S A O