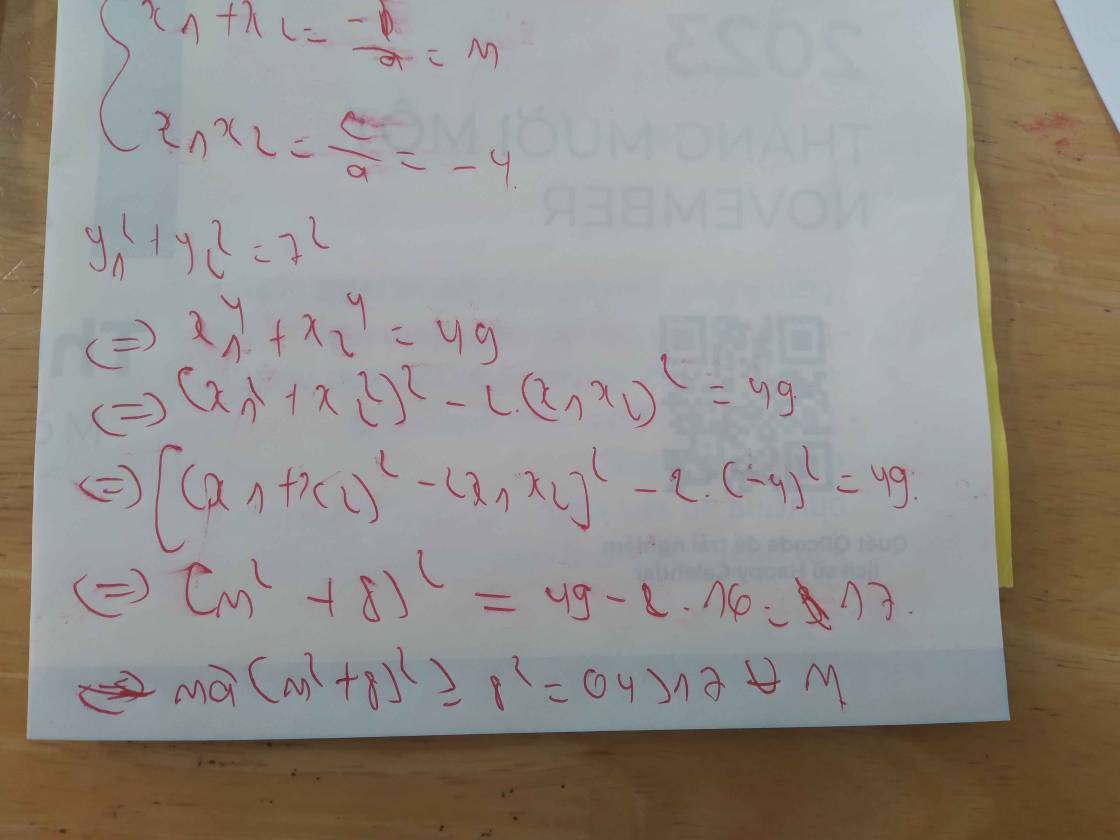Cho parabol (P): y=x2 và đường thẳng (d): 3mx + 4. Gọi x1,x2 là các hoành độ giao điểm.Tìm M để \(\left|\frac{x1}{x2}\right|=4\)
Giúp mình với mình cần gấp!!!

Những câu hỏi liên quan
Cho parabol (P): y=x2 và đường thẳng (d): 3mx + 4. Gọi x1,x2 là các hoành độ giao điểm.Tìm M để \(\left|\frac{x1}{x2}\right|=4\)
Giúp mình với mình cần gấp!!!
Cho parabol (p):y=x^2 và đường thẳng (d):y=-4x+2m-1(Với m là tham số) .Gọi x1 và x2 là hoành độ giao điểm của (p) và (d ) . tìm m để x1^2 -x2 =2m .Mọi người giải hộ mình vs mai mình cần rồi!
Bài 1: Cho parabol (P) : y = x2 và đường thẳng (d) : y= 3mx + 1 - m2 ( m là tham số).
Tìm m để (d) m cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 thõa mãn : x1 + x2 = 2x1x2
(mink đag cần gấp)
Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=3mx+1-m^2\)
\(\Leftrightarrow x^2-3mx+m^2-1=0\)
Để (d) cắt (P) tại hai điểm phân biệt thì phương trình hoành độ giao điểm của (P) và (d) có hai nghiệm phân biệt
\(\Leftrightarrow\text{Δ}\ge0\)
\(\Leftrightarrow\left(-3m\right)^2-4\cdot1\cdot\left(m^2-1\right)\ge0\)
\(\Leftrightarrow9m^2-8m^2+4\ge0\)
\(\Leftrightarrow m^2+4\ge0\)(luôn đúng)
Suy ra: (P) và (d) luôn cắt nhau tại hai điểm phân biệt với mọi m
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1\cdot x_2=m^2-1\\x_1+x_2=3m\end{matrix}\right.\)
Theo đề, ta có phương trình: \(3m=2\cdot\left(m^2-1\right)\)
\(\Leftrightarrow2m^2-2-3m=0\)
\(\Leftrightarrow2m^2-4m+m-2=0\)
\(\Leftrightarrow2m\left(m-2\right)+\left(m-2\right)=0\)
\(\Leftrightarrow\left(m-2\right)\left(2m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\2m+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\2m=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=-\dfrac{1}{2}\end{matrix}\right.\)
Vậy: Để (d) cắt (P) tại hai điểm phân biệt có hoành độ \(x_1;x_2\) thỏa mãn \(x_1+x_2=2x_1x_2\) thì \(m\in\left\{2;-\dfrac{1}{2}\right\}\)
Đúng 2
Bình luận (0)
Xét phương trình hoành độ giao điểm parabol $(P)$ và đường thẳng $(d)$
Có: $x^2=3mx+1-m^$
$⇔x^2-3mx+m^2-1=0(1)$
Xét phương trình (1) có dạng $ax^2+bx+c=0$ với
$\begin{cases}a=1 \neq 0\\b=-3m\\c=m^2-1\end{cases}$
$⇒pt(1)$ là phương trình bậc hai một ẩn $x$
Có $\delta=b^2-4ac=9m^2-4.1.(m^2-1)=5m^2+4>0 \forall m$
suy ra $pt(1)$ có 2 nghiệm phân biệt $x_1;x_2$
Theo hệ thức Viete có: $\begin{cases}x_1+x_2=\dfrac{-b}{a}=3m\\x_1.x_2=\dfrac{c}{a}=m^2-1\end{cases}$
Nên $x_1+x_2=2x_1.x_2$
$⇔3m=2.(m^2-1)$
$⇔2m^2-3m-2=0$
$⇔(m-2)(2m+1)=0$
$⇔$\(\left[{}\begin{matrix}m=2\\m=\dfrac{-1}{2}\end{matrix}\right.\)
Vậy $m∈2;\dfrac{-1}{2}$ thỏa mãn đề
Đúng 1
Bình luận (0)
Cho parabol (P): y = x2 và đường thẳng (d): y = 2mx + 3. Gọi x1; x2 là hoành độ giao điểm của (d) và (P). Tìm m để |x1| + 3|x2| = 6
Phương trình hoành độ giao điểm của \(\left(d\right)\) và \(\left(P\right)\) là:
\(x^2=2mx+3\Leftrightarrow x^2-2mx-3=0\) (1)
Phương trình (1) có hệ số \(a.c=1.\left(-3\right)=-3< 0\) nên (1) luôn có hai nghiệm phân biệt \(x_1,x_2\).
Theo hệ thức Viete ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-3\end{matrix}\right.\)
Ta có: \(\left|x_1\right|+3\left|x_2\right|=6\)
Ta có hệ:
\(\left\{{}\begin{matrix}x_1x_2=-3\\\left|x_1\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\\left|\dfrac{3}{x_2}\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\x_2^2-2\left|x_2\right|+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2=-1,x_1=3\\x_2=1,x_1=-3\end{matrix}\right.\)
Với \(x_1=3,x_2=-1\Rightarrow x_1+x_2=2\Rightarrow m=1\).
Với \(x_1=-3,x_2=1\Rightarrow x_1+x_2=-2\Rightarrow m=-1\)
Đúng 0
Bình luận (0)
Phương trình hoành độ giao điểm của và là:
(1)
Phương trình (1) có hệ số nên (1) luôn có hai nghiệm phân biệt .
Theo hệ thức Viete ta có:
Ta có:
Ta có hệ:
Với .
Với
Đúng 0
Bình luận (0)
bài 1 Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y 2(m-1)x + 3 và parabol (P): y x2 3) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m 4) Gọi x1, x2 là hoành độ các giao điểm của (d) và (P). Tìm m để |x1| + |x2| 4Bài 10: Trong mặt phẳng toạ độ Oxy cho parabol (P) : y x2 và đường thẳng (d):y mx +4. a) Chứng minh rằng với mọi giá trị của m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A( X1;y1) và B(x2;y2). b) Tìm tất cả các giá trị của m sao cho y mũ 2...
Đọc tiếp
bài 1 Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = 2(m-1)x + 3 và parabol (P): y = x2 3) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m 4) Gọi x1, x2 là hoành độ các giao điểm của (d) và (P). Tìm m để |x1| + |x2| = 4
Bài 10: Trong mặt phẳng toạ độ Oxy cho parabol (P) : y = x2 và đường thẳng (d):y = mx +4. a) Chứng minh rằng với mọi giá trị của m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A( X1;y1) và B(x2;y2). b) Tìm tất cả các giá trị của m sao cho y mũ 2 1 + y mũ 2 2 = 7 mũ 2
em cần gấp ạ, cảm ơn ạ
Trên mặt phẳng Oxy, cho đường thẳng (d): y = -4 + m2 - 2 và parabol (P): y = x2
a) Chứng minh đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt với mọi m
b) Gọi x1, x2 là hoành độ hai giao điểm của (d) và (P). Tìm m để x1 ≤ 0 < x2
trên mặt phẳn toạ độ Oxy cho parabol (P):y=x^2 và đường thẳng (d): y=2(m 1)x-2m 4 a)tìm toạ độ giao điểm của (P) và (d) khi m=2 b) gọi x1 và x2 là hoành độ các giao điểm của (P) và (d).cm biểu thức A=x1(1-x2/2) x2(1-x1/2) không phụ thuộc m
Xem chi tiết
Bài 1: Cho parabol (P) : y = x2 và đường thẳng (d) : y= 3mx + 1 - m2 ( m là tham số)
a) TÌm m để (d) đường thẳng đi qua A( 1; -9)
b) Tìm m để (d) m cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 thõa mãn x1 + x2 = 2x1x2
Bài 1:
a) Để (d) đi qua A(1;-9) thì
Thay x=1 và y=-9 vào (d), ta được:
\(3m\cdot1+1-m^2=-9\)
\(\Leftrightarrow-m^2+3m+1+9=0\)
\(\Leftrightarrow m^2-3m-10=0\)
\(\Leftrightarrow m^2-5m+2m-10=0\)
\(\Leftrightarrow m\left(m-5\right)+2\left(m-5\right)=0\)
\(\Leftrightarrow\left(m-5\right)\left(m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-5=0\\m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=5\\m=-2\end{matrix}\right.\)
Vậy: Để (d) đi qua A(1;-9) thì \(m\in\left\{5;-2\right\}\)
Đúng 0
Bình luận (0)
Cho Parabol (P) : y = x2 và đường thẳng (d) : y = mx - m +1
a. Tìm toạ độ giao điểm của (P) và (d) khi m = 4
b. Gọi x1 và x2 là hoành độ giao điểm của (P) và (d) . Tìm m sao cho x1 = 9 x2
a. Bạn tự giải
b. Pt hoành độ giao điểm: \(x^2=mx-m+1\Leftrightarrow x^2-mx+m-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)-m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1-m\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=m-1\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x_1=1\\x_2=m-1\end{matrix}\right.\) \(\Rightarrow1=9\left(m-1\right)\Rightarrow m=\dfrac{10}{9}\)
TH2: \(\left\{{}\begin{matrix}x_1=m-1\\x_2=1\end{matrix}\right.\) \(\Rightarrow m-1=9.1\Rightarrow m=10\)
Đúng 2
Bình luận (0)