giải phương trình :
\(x^4-3\text{x}^3+4\text{x}^2-3\text{x}+1=0\)
Giải các bất phương trình sau
1) \(\sqrt{\text{x}^2+1}< 3\) 2) \(\dfrac{\text{x^2}-4x+3}{x^2-4}< 0\)
\(1)\sqrt{x^2+1}< 3.\\ \Leftrightarrow x^2+1< 9.\\ \Leftrightarrow x^2< 8.\\ \Leftrightarrow\left[{}\begin{matrix}x< 2\sqrt{2}.\\x>-2\sqrt{2}.\end{matrix}\right.\)
\(\Leftrightarrow-2\sqrt{2}< x< 2\sqrt{2}.\)
\(2)\dfrac{x^2-4x+3}{x^2-4}< 0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-4x+3}{x^2-4}.\)
\(x^2-4=0.\Leftrightarrow\left[{}\begin{matrix}x=2.\\x=-2.\end{matrix}\right.\\ x^2-4x+3=0.\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=1.\end{matrix}\right.\)
Bảng xét dấu:
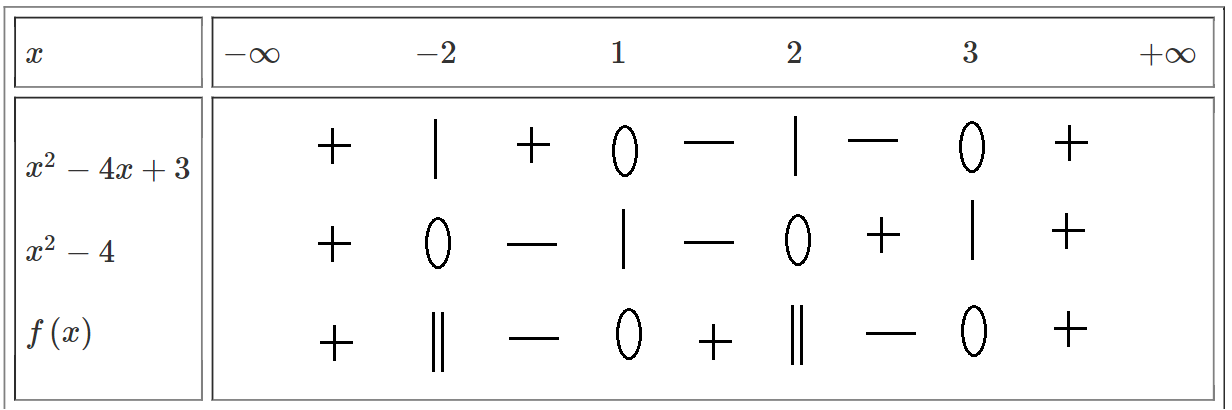
\(\Rightarrow f\left(x\right)< 0\Leftrightarrow x\in\left(-2;1\right)\cup\left(2;3\right).\)
Lời giải:
1.
$\sqrt{x^2+1}<3$
$\Leftrightarrow 0\leq x^2+1<9$
$\Leftrightarrow x^2+1<9$
$\Leftrightarrow x^2<8$
$\Leftrightarrow -2\sqrt{2}< x< 2\sqrt{2}$
2.
Xét 2 TH:
TH1: \(\left\{\begin{matrix} x^2-4x+3<0\\ x^2-4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x-1)(x-3)<0\\ (x-2)(x+2)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 1< x< 3\\ x>2 \text{hoặc} x<-2\end{matrix}\right.\)
\(\Leftrightarrow 2< x<3\)
TH2: \(\left\{\begin{matrix} x^2-4x+3>0\\ x^2-4<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x-1)(x-3)>0\\ (x-2)(x+2)<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>3 \text{hoặc} x<1\\ -2< x< 2\end{matrix}\right.\)
\(\Leftrightarrow -2< x< 1\)
Kết hợp 2 TH suy ra tập nghiệm \(S=(2;3)\cup (-2;1)\)
\(\frac{1}{x^2+1}+\frac{1}{x^2+2}+\frac{1}{x^2+3}+\frac{1}{x^2+4}=0\)Giải phương trình .
Do \(x^2\ge0\Rightarrow x^2+1\ge1\Rightarrow\frac{1}{x^2+1}>0.\)
Tương tự \(\frac{1}{x^2+2};\frac{1}{x^2+3};\frac{1}{x^2}+4>0\)
=> Phương trình vô nghiệm
Giải bất phương trình:
\(\text{ a) }\left|3x-2\right|< 4\)
\(\text{b) }\left|3-2x\right|< x+1\)
\(\text{c) }\left|3x-1\right|>5\)
\(\text{d) }\left|x+1\right|>\left|x-2\right|\)
\(\text{e) }\left|x-1\right|+\left|x-5\right|>8\)
Giải các bất phương trình sau
1) \(\dfrac{\text{x - 2}}{x+1}-\dfrac{3}{x+2}>0\) 2) \(\dfrac{\text{x + 1}}{x+2}+\dfrac{x}{x-3}\le0\)
3) \(\dfrac{\text{x}^2+2x+5}{x+4}>x-3\) 4) \(\sqrt{\text{x^2}-3x+2}\ge3\)
\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
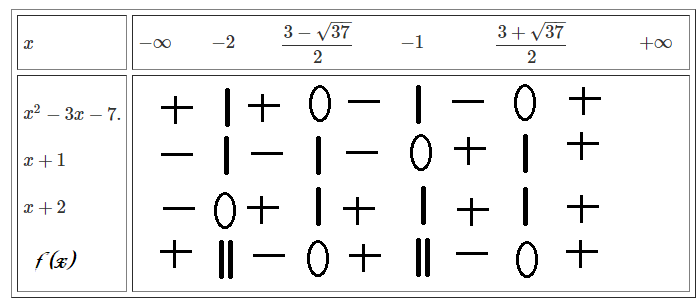
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
giải phương trình:
\(\sqrt{3\text{x}^{2^{ }}-5\text{x}+1}-\sqrt{\text{x}^2-2}=\sqrt{3\left(\text{x}^2-\text{x}-1\right)}-\sqrt{\text{x}^{2^{ }}-3\text{x}+4}\)
ĐKXĐ \(3x^2-5x+1\ge0;x^2-2\ge0;x^2-x-1\ge0\)
Ta có : \(\sqrt{3x^2-5x+1}-\sqrt{x^2-2}=\sqrt{3.\left(x^2-x-1\right)}-\sqrt{x^2-3x+4}\)
\(\Leftrightarrow\sqrt{3x^2-5x+1}-\sqrt{3\left(x^2-x-1\right)}=\sqrt{x^2-2}-\sqrt{x^2-3x+4}\)
\(\Leftrightarrow\dfrac{3x^2-5x+1-3.\left(x^2-x-1\right)}{\sqrt{3x^2-5x+1}+\sqrt{3\left(x^2-x-1\right)}}=\dfrac{x^2-2-x^2+3x-4}{\sqrt{x^2-2}+\sqrt{x^2-3x+4}}\)
\(\Leftrightarrow\dfrac{-2x+4}{\sqrt{3x^2-5x+1}+\sqrt{3\left(x^2-x-1\right)}}=\dfrac{3x-6}{\sqrt{x^2-2}+\sqrt{x^2-3x+4}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\\dfrac{3}{\sqrt{x^2-2}+\sqrt{x^2-3x+4}}+\dfrac{2}{\sqrt{3x^2-5x+1}+\sqrt{3\left(x^2-x-1\right)}}=0\left(∗\right)\end{matrix}\right.\)
Xét phương trình (*) ta có VT > 0 \(\forall x\) mà VP = 0
nên (*) vô nghiệm
Vậy x = 2 là nghiệm phương trình
giải phương trình sau :
\(\sqrt{x}+\sqrt[4]{x\text{(}1-x\text{)}^2}+\sqrt[4]{\text{(}1-x\text{)}^3}=\sqrt{1-x}+\sqrt[4]{x^3}+\sqrt[4]{x^2.\text{(}1-x\text{)}}\)
Giải phương trình
\(4\text{x}^4-\text{x}^3-16\text{x}^2+4\text{x}-1995=0\)
\(pt\Leftrightarrow\left(x-5\right)\left(4x^3+19x^2+79x+399\right)=0\)
giải phương trình
\(\text{x}^2-4=3\sqrt{\text{x}^3-4\text{x}}\)
\(9\text{x}+17=6\sqrt{8\text{x}-1}+4\sqrt{\text{x}+3}\)
\(\sqrt{2\text{x}-1}+\text{x}=\sqrt{\text{x}}+\sqrt{\text{x}^2-\text{x}+1}\)
\(2\sqrt{\text{x}^2-\text{x}+1}+\sqrt{\text{x}^2+\text{x}+1}=\sqrt{\text{x}^4+\text{x}^2+1}+2\)
a: Đặt \(x^2-4=a\)
Pt sẽ là \(a=3\sqrt{xa}\)
\(\Rightarrow a^2=9xa\)
\(\Leftrightarrow a\left(a-9x\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(x^2-4-9x\right)=0\)
hay \(x\in\left\{2;-2;\dfrac{9+\sqrt{97}}{2};\dfrac{9-\sqrt{97}}{2}\right\}\)
d: Đặt \(\sqrt{x^2-x+1}=a;\sqrt{x^2+x+1}=b\)
Pt sẽ là 2a+b=ab+2
=>(b-2)(1-a)=0
=>b=2 và 1-a
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+x+1=4\\x^2-x+1=1\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
Bài 1 : Giải phương trình bằng cách đưa về phương trình tích
a) (2x+1) (3x-2) = (5x-8) (2x+1)
b) (4x^2-1) = (2x+1) (3x-5)
c) (x+1)^2 = 4 . (x^2-2x+1)
d) 2x^3 + 5x^2 - 3x = 0
Bài 2 : Giải phương trình :
a) 1/2x-3 - 3/x.(2x-3) = 5/x
b) x+2/x-2 - 1/x = 2/x.(x-2)
c) x+1/x-2 + x-1/x+2 = 2(x^2+2)/x^2-4
Bài 3 : Giải phương trình :
x^4 + x^3 + 3x^2 + 2x + 2 = 0
Help mee
câu a bài 1:(2x+1)(3x-2)=(5x-8)(2x+1)
<=>(2x+1)(3x-2)-(5x-8)(2x+1)=0
<=>(2x+1)(3x-2-5x+8)=0
<=>(2x+1)(6-2x)=0
bước sau tự làm nốt nha !
câu b:gợi ý: tách 4x^2-1thành (2x-1)(2x+1) rồi làm như câu a
Bài 2:
a: \(\dfrac{1}{2x-3}-\dfrac{3}{x\left(2x-3\right)}=\dfrac{5}{x}\)
\(\Leftrightarrow x-3=5\left(2x-3\right)=10x-15\)
=>-9x=-12
hay x=4/3
b: \(\Leftrightarrow x\left(x+2\right)-x+2=2\)
=>x2+2x-x+2=2
=>x2+x=0
=>x=0(loại) hoặc x=-1(nhận)
c: \(\dfrac{x+1}{x-2}+\dfrac{x-1}{x+2}=\dfrac{2\left(x^2+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow x^2+3x+2+x^2-3x+2=2x^2+4\)
=>4=4(luôn đúng)
Vậy: S={x|x<>2; x<>-2}