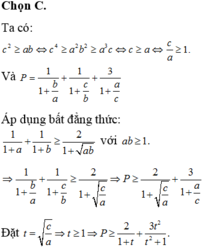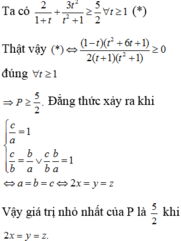Cho x, y, z là các số thực dương sao cho x+y+z=3. Tìm giá trị nhỏ nhất của P=x2+y2+z2+xyz

Những câu hỏi liên quan
Cho x,y,z là 3 số thực dương thỏa mãn x+y+z=1. Xác định giá trị nhỏ nhất của biểu thức?
P=\(\frac{1}{\left(x2+y2+z2\right)}+\frac{1}{xyz}\)
Cho 3 số thực dương x, y, z thỏa mãn:
1
x
2
+
1
y
2
+
1
z
2
1
. Tìm giá trị nhỏ nhất của biểu thức:
P
y
2
z
2
x
(
y
2...
Đọc tiếp
Cho 3 số thực dương x, y, z thỏa mãn: 1 x 2 + 1 y 2 + 1 z 2 = 1 . Tìm giá trị nhỏ nhất của biểu thức: P = y 2 z 2 x ( y 2 + z 2 ) + z 2 x 2 y ( z 2 + x 2 ) + x 2 y 2 z ( x 2 + y 2 )
Ta có:
P = 1 x ( 1 z 2 + 1 y 2 ) + 1 y ( 1 z 2 + 1 x 2 ) + 1 z ( 1 x 2 + 1 y 2 )
Đặt: 1 x = a ; 1 y = b ; 1 z = c thì a,b,c>0 và a2+b2+c2=1
P = a b 2 + c 2 + b c 2 + a 2 + c a 2 + b 2 = a 2 a ( 1 − a 2 ) + b 2 b ( 1 − b 2 ) + c 2 c ( 1 − c 2 )
Áp dụng bất đẳng thức Côsi cho 3 số dương ta có:
a 2 1 - a 2 2 = 1 2 .2 a 2 ( 1 − a 2 ) ( 1 − a 2 ) ≤ 1 2 2 a 2 + 1 − a 2 + 1 − a 2 3 = 4 27 = > a ( 1 − a 2 ) ≤ 2 3 3 < = > a 2 a ( 1 − a 2 ) ≥ 3 3 2 a 2 ( 1 )
Tương tự: b 2 b ( 1 − b 2 ) ≥ 3 3 2 b 2 ( 2 ) ; c 2 c ( 1 − c 2 ) ≥ 3 3 2 c 2 ( 3 )
Từ (1); (2); (3) ta có P ≥ 3 3 2 ( a 2 + b 2 + c 2 ) = 3 3 2
Đẳng thức xảy ra a = b = c = 1 3 h a y x = y = z = 3
Vậy giá trị nhỏ nhất của P là 3 3 2
Đúng 0
Bình luận (0)
cho các số thực x, y ,z không âm thoả mãn : x2+y2+z2=1 .
Tìm giá tri nhỏ nhất và giá tri lớn nhất của \(A=\sqrt{x+y}+\sqrt{y+z}+\sqrt{z+x}\)
\(A\le\sqrt{3\left(x+y+y+z+z+x\right)}=\sqrt{6\left(x+y+z\right)}\le\sqrt{6.\sqrt{3\left(x^2+y^2+z^2\right)}}=\sqrt{6\sqrt{3}}\)
\(A_{max}=\sqrt{6\sqrt{3}}\) khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)
Do \(x^2+y^2+z^2=1\Rightarrow0\le x;y;z\le1\)
\(\Rightarrow\left\{{}\begin{matrix}x^2\le x\\y^2\le y\\z^2\le z\end{matrix}\right.\) \(\Rightarrow x+y+z\ge x^2+y^2+z^2=1\)
\(A^2=2\left(x+y+z\right)+2\sqrt{\left(x+y\right)\left(x+z\right)}+2\sqrt{\left(x+y\right)\left(y+z\right)}+2\sqrt{\left(y+z\right)\left(z+x\right)}\)
\(A^2=2\left(x+y+z\right)+2\sqrt{x^2+xy+yz+zx}+2\sqrt{y^2+xy+yz+zx}+2\sqrt{z^2+xy+yz+zx}\)
\(A^2\ge2\left(x+y+z\right)+2\sqrt{x^2}+2\sqrt{y^2}+2\sqrt{z^2}=4\left(x+y+z\right)\ge4\)
\(\Rightarrow A\ge2\)
\(A_{min}=2\) khi \(\left(x;y;z\right)=\left(0;0;1\right)\) và các hoán vị
Đúng 0
Bình luận (0)
cho các số thực x, y ,z không âm thoả mãn : x2+y2+z2=1 . tìm giá tri nhỏ nhất và giá tri lớn nhất của P = √ (x^2 + y^2) + √(y^2 + z^2) + √ (z^2 + x^2)
Cho các số thực dương x,y,z. Tìm giá trị nhỏ nhất của biểu thức P= (xy+yz+zx) / (x²+y²+z²) + (x+y+z)³ / xyz
Cho các số thực dương x, y, z thỏa mãn x + y + z = 4.Tìm giá trị nhỏ nhất của biểu thức P = \(\dfrac{x+z}{xyz}\)
Có \(P=\dfrac{x+z}{xyz}=\dfrac{1}{yz}+\dfrac{1}{xy}=\dfrac{1}{y}\left(\dfrac{1}{x}+\dfrac{1}{z}\right)\ge\dfrac{1}{y}.\dfrac{4}{x+z}\)
\(=\dfrac{4}{y\left(x+z\right)}=\dfrac{4}{y\left(4-y\right)}=\dfrac{4}{-y^2+4y}=\dfrac{4}{-\left(y-2\right)^2+4}\ge1\)
"=" xảy ra khi y = 2 ; x = 1 ; z = 1
Đúng 2
Bình luận (0)
Ta có x+y+z=4
=>y=4-x-z
Ta có :x,y,z>0
=>\(x^2>0,z^2>0\)
=>\(x^2z>0,z^2x>0\)
Áp dụng bất đẳng thức cô si với hai số dương \(x^2z\) và z ta có
\(x^2z+z\)>=2\(\sqrt{x^2z.z}\)
<=>\(x^2z+z>=2xz\)
CMTT:\(z^2x+x>=2xz\)
=>\(x^2z+z+z^2x+x>=4xz\)
=>\(x+z>=4xz-x^2z-z^2x\)
=>\(x+z>=xz\left(4-x-z\right)\)
Mà y=4-x-z(cmt)
=>\(x+z>=xyz\)
=>\(\dfrac{x+z}{xyz}>=1\)
hay \(P>=1\)
Dấu "=" xảy ra <=> \(\left\{{}\begin{matrix}x^2z=z\\z^2x=x\\x+y+z=4\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x^2=1\\z^2=1\\x+y+z=4\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=1\\z=1\\1+y+1=4\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=1\\z=1\\y=2\end{matrix}\right.\)
Vậy tại x=1, y=2,z=1 thì P có giá trị nhỏ nhất là 1
Đúng 0
Bình luận (0)
Cho x, y, z là các số thực dương thỏa mãn điều kiện
y
2
≥
2
x
z
;
z
2
≥
2
x
y
. Giá trị nhỏ nhất của biểu thức:
P
2
x
2
x
+
y
+
y
y...
Đọc tiếp
Cho x, y, z là các số thực dương thỏa mãn điều kiện y 2 ≥ 2 x z ; z 2 ≥ 2 x y . Giá trị nhỏ nhất của biểu thức: P = 2 x 2 x + y + y y + z + 3 z z + 2 x nằm trong khoảng nào sau đây?
A. (0;1)
B. (1;2)
C. (2;3)
D. (3;4)
a) Cho x,y,z là các số dương thỏa mãn x2+y2+z23, tìm giá trị nhỏ nhất của Fdfrac{x^2+1}{z+2}+dfrac{y^2+1}{x+2}+dfrac{z^2+1}{y+2}
b) Với a,b,c 0 thỏa mãn ab+bc+ca3, chứng minh rằng
sqrt{dfrac{a}{a+3}} +sqrt{dfrac{b}{b+3}}+sqrt{dfrac{c}{c+3}}ledfrac{3}{2}
Đọc tiếp
a) Cho x,y,z là các số dương thỏa mãn x2+y2+z2=3, tìm giá trị nhỏ nhất của F=\(\dfrac{x^2+1}{z+2}\)+\(\dfrac{y^2+1}{x+2}\)+\(\dfrac{z^2+1}{y+2}\)
b) Với a,b,c > 0 thỏa mãn ab+bc+ca=3, chứng minh rằng
\(\sqrt{\dfrac{a}{a+3}}\) +\(\sqrt{\dfrac{b}{b+3}}\)+\(\sqrt{\dfrac{c}{c+3}}\)\(\le\)\(\dfrac{3}{2}\)
Cho các số thực dương x, y, z thỏa mãn
e
x
+
y
+
z
≤
e
x
+
y
+
z
. Tìm giá trị nhỏ nhất của biểu thức
P
4
x
-
z...
Đọc tiếp
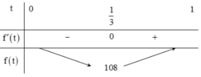
Cho các số thực dương x, y, z thỏa mãn e x + y + z ≤ e x + y + z . Tìm giá trị nhỏ nhất của biểu thức P = 4 x - z 2 + 4 x z + 1 y 3
A. 108
B. 106
C. 268
D. 106
Chọn đáp án A
Xét hàm số
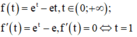
Ta có bảng biến thiên:
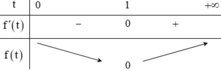

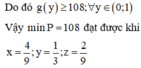
Đúng 0
Bình luận (0)