Đáp án B

Ta có:

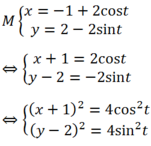
=> ( x +1) ²+ (y- 2) ²= 4cos²t + 4sin²t

=> ( x +1) ²+ (y- 2) ² = 4

Vậy tập hợp điểm M  là phương trình đường tròn có tâm I( -1;2) , bán kính R= 2.

Lời giải:

PT hoành độ giao điểm:

\(x^3-2(m+1)x^2+(5m+1)x-2m-2=0\)

\(\Leftrightarrow (x-2)(x^2-2mx+m+1)=0\)

Vì \(A(2,0)\) nên hoành độ hai điểm \(B,C\) sẽ là nghiệm của PT \(x^2-2mx+m+1=0\)

Điều kiện: \(\Delta'=m^2-(m+1)>0\)

Khi đó, áp dụng định lý Viete, nếu $x_1,x_2$ là hai nghiệm của PT thì \(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m+1\end{matrix}\right.\)

Nhận thấy hai điểm $B,C$ nằm trên $Ox$ mà một điểm nằm trong đường tròn \(x^2+y^2=1\) nên \((x_1-1)(x_2-1)<0\)

\(\Leftrightarrow x_1x_2-(x_1+x_2)+1<0\Leftrightarrow m+1-2m+1<0\)

\(\Leftrightarrow m>2\). Thử lại ta thấy thỏa mãn điều kiện \(\Delta'\)

Vậy \(m>2\)

Ta có :

x = 5y => \(\frac{x}{5}=y\)

Áp dụng t/c của dãy tỉ số bằng nhau, ta có : 

\(\frac{x}{5}=\frac{y}{1}=\frac{x+y}{5+1}=\frac{42}{6}=7\)

Suy ra :

+) \(\frac{x}{5}=7\Leftrightarrow x=35\)

+) \(y=7\)

Vậy x = 35 ; y = 7

Mình cảm ơn ạ ^^

Gọi \(A\left(x_1;x_1^2\right)\) và \(B\left(x_2;x_2^2\right)\) là 2 điểm thuộc (P) và đối xứng qua M

Do A; B đối xứng qua M

\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2.\left(-1\right)\\x_1^2+x_2^2=2.5\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x_2=-2-x_1\\x_1^2+x_2^2=10\end{matrix}\right.\)

\(\Rightarrow x_1^2+\left(-2-x_1\right)^2=10\)

\(\Rightarrow2x_1^2+4x_1-6=0\Rightarrow\left[{}\begin{matrix}x_1=1\\x_1=-3\end{matrix}\right.\)

Vậy 2 điểm đó là \(\left(1;1\right)\) và \(\left(-3;9\right)\)

Chọn A

Lời giải:

PT hoành độ giao điểm:

\(x^2(m-1)+x(12-7m)+(10m-29)=0(1)\)

Để hai đồ thị hàm số cắt nhau tại hai điểm phân biệt thì PT $(1)$ phải có hai nghiệm phân biệt \(\Leftrightarrow \left\{\begin{matrix} m\neq 1\\ \Delta=(12-7m)^2-4(m-1)(10m-29)>0\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} m\neq 1\\ 9m^2-12m+28=(3m-2)^2+24>0\end{matrix}\right.\Leftrightarrow m\neq 1\)

Khi đó , áp dụng định lý Viete, nếu $x_1,x_2$ là hai nghiệm của $(1)$ thì: \(x_1+x_2=\frac{7m-12}{m-1}\)

Hai giao điểm của hai ĐTHS là \(A(x_1,m(x_1-5)+10);B(x_2,m(x_2-5)+10)\)

\(M(5,10)\) là trung điểm của $AB$

\(\Leftrightarrow \left\{\begin{matrix} \frac{x_1+x_2}{2}=5\\ \frac{y_1+y_2}{2}=\frac{m(x_1+x_2)-10m+20}{2}=10\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{7m-12}{m-1}=10\\ \frac{m(7m-12)}{m-1}=10m\end{matrix}\right.\)

Suy ra \(m=\frac{-2}{3}\) (thỏa mãn)