\(x^4-2x^3+4x^2-3x+2=0\\ \Leftrightarrow x^4-2x^3+x^2+3x^2-3x+2=0\\ \Leftrightarrow x^2\left(x^2-2x+1\right)+\left(3x^2-3x+2\right)=0\\ \Leftrightarrow x^2\left(x-1\right)^2+\left(3x^2-3x+2\right)=0\)

Vì \(x^2\left(x-1\right)^2\ge0\) và dễ dàng chứng minh được \(3x^2-3x+2>0\) nên pt vô nghiệm

Chứng minh rằng phương trình sau có ít nhất hai nghiệm : 

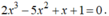
- Xét hàm số: f ( x ) = 2 x 3 - 5 x 2 + x + 1  là hàm đa thức.

⇒ Hàm số f liên tục trên R.

- Ta có:

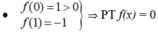 có ít nhất một nghiệm c1 ∈ (0;1).

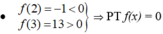 có ít nhất một nghiệm c2 ∈ (2;3).

- Mà c   ≠   c 2  nên PT f(x) = 0 có ít nhất 2 nghiệm.

pt<=>x^2-2x.1/2+1/4-1/4+12/4=0

<=> (x-1/2)^2+11/4>=11/4>0

=>phương trình vô nghiệm

Ta có : x^2 - x +3 = 0 

     <=>x(x-1)=-3

    Vì x(x-1) là 2 số tự nhiên liên tiếp nên chia hết cho 2 

 Mà 3 không chia hết cho 2 

=> vậy phương trình trên vô nghiệm

x 4 − 5 x 3 + 8 x 2 − 10 x + 4 = 0 ⇔ ( x 4 + 4 x 2 + 4 ) − 5 x 3 + 4 x 2 − 10 x = 0

⇔ x 2 + 2 2 − 5 x 3 + 10 x + 4 x 2 = 0 ⇔ x 2 + 2 2 − 5 x x 2 + 2 + 4 x 2 = 0

Đặt t = x 2 + 2  ta được t 2 − 5 t x + 4 x 2 = 0 ⇔ t − x t − 4 x = 0

Hay phương trình đã cho ⇔ x 2 − x + 2 x 2 − 4 x + 2 = 0

⇔ x 2 − x + 2 = 0    ( V N ) x 2 − 4 x + 2 = 0 ⇔ x = 2 ± 2

Vậy phương trình không có nghiệm nguyên

Đáp án cần chọn là: D

Đặt f(x) = 2x3 – 6x + 1

TXĐ: D = R

f(x) là hàm đa thức nên liên tục trên R.

Ta có: f(-2) = 2.(-2)3 – 6(-2) + 1 = - 3 < 0

            f(0) = 1 > 0

            f(1) = 2.13 – 6.1 + 1 = -3 < 0.

⇒ f(-2).f(0) < 0 và f(0).f(1) < 0

⇒ f(x) = 0 có ít nhất một nghiệm thuộc khoảng (-2; 0) và ít nhất một nghiệm thuộc (0 ; 1)

⇒ phương trình f(x) = 0 có ít nhất hai nghiệm.

Phương trình (1) vô nghiệm khi phương trình (2) có 2 nghiệm số âm hoặc vô nghiệm.

Nếu phương trình (2) có 2 nghiệm âm thì theo hệ thức Vi-ét ta có:

t 1 + t 2  = 13 > 0 vô lý

Vậy phương trình (1) vô nghiệm khi phương trình (2) vô nghiệm.

Suy ra: ∆ = 169 - 4m < 0 ⇔ m > 169/4}

a) ax^2 + bx + c = 0 Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt. ∆ > 0 => b^2 - 4ac > 0 x1 + x2 = -b/a > 0 => b và a trái dấu x1.x2 = c/a > 0 => c và a cùng dấu Từ đó ta xét phương trình cx^2 + bx^2 + a = 0 ∆ = b^2 - 4ac >0 x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0 x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0 => phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4 Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt. b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si. x1 + x2 ≥ 2√( x1.x2 ) x3 + x4 ≥ 2√( x3x4 ) => x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#) Tiếp tục côsi cho 2 số không âm ta có √( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##) Theo a ta có x1.x2 = c/a x3.x4 = a/c => ( x1.x2 )( x3.x4 ) = 1 => 2√[√( x1.x2 )( x3.x4 ) ] = 2 Từ (#) và (##) ta có x1 + x2 + x3 + x4 ≥ 4

Đáp án: A

Bước 1 sai  vì giả sử phản chứng sai, phải giả sử phương trình vô nghiệm và a, c trái dấu.