Trong Oxy, cho ΔABC vuông cân tại A, có trọng tâm G (\(\frac{2}{3}\);0). Biết M(1;-1) là trung điểm của BC. Tìm tọa độ các đỉnh của ΔABC

Những câu hỏi liên quan
Cho ΔABC có 3 góc và H là trực tâm. Các đường thẳng vuông góc vs AB tại B, vuông góc vs AC tại C cắt nhau tại D
a, Tứ giác BDCH là hình j ?
b, C/m MI = \(\dfrac{1}{2}\)AH biết I là trung điểm BC và đường vuông góc với BC tại I cắt AD tại M
m.n vẽ hình giúp e nữa ạ Thank nhiều
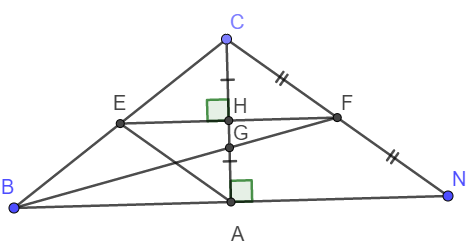
Cho tam giác CBN cân tại C có CA là đường cao, CA15cm, BC25cm a)Tính AB và so sánh các góc trong tam giác ABC.b)Gọi H là trung điểm AC, tại H vẽ đường vuông góc với AC, cắt BC tại E. C/m tam giác EHAtam giác EHC và tam giác ABE cân tại A.C)Gọi F là trung điểm NC, BF cắt AC tại G. C/m G là trọng tâm tam giác BCN và tính AG.d)C/m E,H,F thẳng hàng.Ai làm trước mih tck cho :))
Đọc tiếp
Cho tam giác CBN cân tại C có CA là đường cao, CA=15cm, BC=25cm
a)Tính AB và so sánh các góc trong tam giác ABC.
b)Gọi H là trung điểm AC, tại H vẽ đường vuông góc với AC, cắt BC tại E. C/m tam giác EHA=tam giác EHC và tam giác ABE cân tại A.
C)Gọi F là trung điểm NC, BF cắt AC tại G. C/m G là trọng tâm tam giác BCN và tính AG.
d)C/m E,H,F thẳng hàng.
Ai làm trước mih tck cho :))
a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 \(\Rightarrow ab=20\left(cm\right)\)
Xét tam giác ABC có:
AC < AB < BC nên \(\widehat{CBA}< \widehat{BCA}< \widehat{BAC}.\)
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
\(\Rightarrow\Delta EHC=\Delta EHA\) (Hai cạnh góc vuông)
Do \(\Delta EHC=\Delta EHA\Rightarrow\widehat{ECA}=\widehat{EAC}\)
\(\Rightarrow\widehat{EBA}=\widehat{EAB}\) (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
\(\frac{AG}{AC}=\frac{1}{3}\Rightarrow AG=\frac{1}{5}.15=5\left(cm\right)\)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có \(\Delta ECH=\Delta F'CH\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow CE=CF'\)
Lại có \(CE=\frac{1}{2}BC=\frac{1}{2}CN\Rightarrow CF'=\frac{1}{2}CN\)
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.
Đúng 0
Bình luận (0)
Bài giải :

a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 ⇒ab=20(cm)
Xét tam giác ABC có:
AC < AB < BC nên ^CBA<^BCA<^BAC.
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
⇒ΔEHC=ΔEHA (Hai cạnh góc vuông)
Do ΔEHC=ΔEHA⇒^ECA=^EAC
⇒^EBA=^EAB (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
AGAC =13 ⇒AG=15 .15=5(cm)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có ΔECH=ΔF'CH (Cạnh góc vuông và góc nhọn kề)
⇒CE=CF'
Lại có CE=12 BC=12 CN⇒CF'=12 CN
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.
Đúng 0
Bình luận (0)
Không có hình cũng được ạ.
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Gọi H là giao điểm của đường trung tuyến CM với OA. Gọi G là trọng tâm của tam giác AMC. CMR:
a) OM vuông góc GH
b) OG vuông góc CM
Trong mặt phẳng với hệ trục tọa độ Oxy; tam giác ABC có đỉnh A( 2;-3) ; B( 3;-2) và diện tích tam giác ABC bằng 3/2. Biết trọng tâm G của tam giác ABC thuộc đường thẳng d: 3x- y- 8 0. Tìm tọa độ điểm C. A. C( -1; 1) và C( 2 ; -3) B. C( 1;-1)và C( -2 ; 10) C. ( 1;-1) và C(2 ; -6) D. C( 1;1) và C( 2 ; -3)
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy; tam giác ABC có đỉnh A( 2;-3) ; B( 3;-2) và diện tích tam giác ABC bằng 3/2. Biết trọng tâm G của tam giác ABC thuộc đường thẳng d: 3x- y- 8= 0. Tìm tọa độ điểm C.
A. C( -1; 1) và C( 2 ; -3)
B. C( 1;-1)và C( -2 ; 10)
C. ( 1;-1) và C(2 ; -6)
D. C( 1;1) và C( 2 ; -3)
Đáp án B
![]() => Đường thẳng AB có pt là: x- y – 5= 0.
=> Đường thẳng AB có pt là: x- y – 5= 0.
Gọi G(a;3a- 8) suy ra C( 3a- 5; 9a -19).
Ta có:

Vậy C( 1 ; -1) và C( -2 ; 10)
Đúng 0
Bình luận (0)
Bài 1: cho tam giác ABC có AB=7cm; AC=6cm, BC=5cm. Tính khoảng cách từ trọng tâm đến tâm đường trìn nội tiếp.
Bài 2: Cho tam giác ABC nội tiếp (O) đường kính AC. Trên tia AB lấy D sao cho AD=3AB. Đường thẳng Dy vuông góc với DC cắt tiếp tuyến Ax của (O) tại E. CM tam giác BDE cân.
Một con lắc đơn có dây treo có khối lượng không đáng kể, có chiều dài l0,4m treo tại nơi có gia tốc trọng trường g10m/s2 . Tại vị trí cân bằng người ta truyền cho con lắc vận tốc 0,1π m/s hướng sang phải. Chọn chiều dương hướng sang phải, gốc thời gian là lúc vật bắt đầu dao động. Phương trình dao động của vật có dạng?A.α5πcos(5t -π/2)B.απ/20cos(5t-π/2)C.απ/8 cos(5πt + π/2)D.απ/40cos(5t-π/2)
Đọc tiếp
Một con lắc đơn có dây treo có khối lượng không đáng kể, có chiều dài l=0,4m treo tại nơi có gia tốc trọng trường g=10m/s2 . Tại vị trí cân bằng người ta truyền cho con lắc vận tốc 0,1π m/s hướng sang phải. Chọn chiều dương hướng sang phải, gốc thời gian là lúc vật bắt đầu dao động. Phương trình dao động của vật có dạng?
A.α=5πcos(5t -π/2)
B.α=π/20cos(5t-π/2)
C.α=π/8 cos(5πt + π/2)
D.α=π/40cos(5t-π/2)
Cho tam giác abc có ab=5,ac=13,bc=8cm chứng minh tam giác abc vuông tại a
Cho tam giác def có de=6, ef=5,df=7cm hãy so sánh các góc của tam giác def
Cho tam giác abc am là trung tuyến g là trọng tâm tính ag biết am =12cm
Một thanh
A
B
7
,
5
m
có trọng lượng 200 N có trọng tâm G cách đầu A một đoạn 2 m. Thanh có thể quay xung quanh một trục đi qua O. Biết
O
A
2
,
5
m
. Để AB cân bằng phải tác dụng vào đầu B một lực F có độ lớn bằng A. 100 N. B. 25 N. C. 10 N. D. 20 N.
Đọc tiếp
Một thanh A B = 7 , 5 m có trọng lượng 200 N có trọng tâm G cách đầu A một đoạn 2 m. Thanh có thể quay xung quanh một trục đi qua O. Biết O A = 2 , 5 m . Để AB cân bằng phải tác dụng vào đầu B một lực F có độ lớn bằng
A. 100 N.
B. 25 N.
C. 10 N.
D. 20 N.
Chọn D.
Áp dụng quy tắc momen lực:
P.GO = F.BO
![]()
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có góc A=120 độ. Các đường trung trực của AB và AC cắt nhau tại O và cắt BC lần lượt tại E và F. Chứng minh:
a)AO là trung trực của BC
b)E,F là trọng tâm của tgAOB và AOC
c)BE=EF=FC














